20 câu trắc nghiệm GTLN và GTNN lớp 12 dạng đúng sai giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.
Câu 1. Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên:
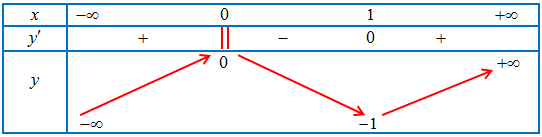
Khi đó:
a) Hàm số có giá trị cực tiểu bằng 1 .
b) Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1 .
c) Hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 1$.
d) Hàm số có đúng một cực trị.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Sai |
Đáp án a sai vì hàm số có giá trị cực tiểu $y = – 1$ khi $x = 0$.
Đáp án b sai vì hàm số không có GTLN và GTNN trên $\mathbb{R}$.
Đáp án c đúng vì hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 1$.
Đáp án d sai vì hàm số có 2 điểm cực trị.
Câu 2. Xét hàm số $y = f\left( x \right)$ với $x \in \left[ { – 1;5} \right]$ có bảng biến thiên như sau:
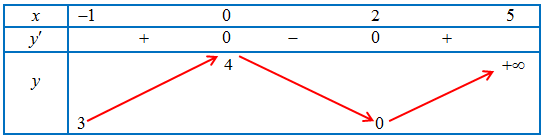
Khi đó:
a. Hàm số đã cho không tồn taị GTLN trên đoạn $\left[ { – 1;5} \right]$
b) Hàm số đã cho đạt GTNN tại $x = – 1$ và $x = 2$ trên đoạn $\left[ { – 1;5} \right]$
c) Hàm số đã cho đồng biến trên khoảng $\left( {2;5} \right)$
d) Hàm số đã cho đạt GTNN tại $x = 0$ trên đoạn $\left[ { – 1;5} \right]$
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
a) Đúng. Vì $\mathop {\lim }\limits_{x \to {5^ – }} y = + \infty $ nên hàm số không có GTLN trên đoạn $\left[ { – 1;5} \right]$.
b) Sai. Hàm số đã cho chỉ đạt GTNN tại $x = 2$ trên đoạn $\left[ { – 1;5} \right]$.
c) Đúng
d) Sai. Hàm số đã cho chỉ đạt GTNN tại $x = 2$ trên đoạn $\left[ { – 1;5} \right]$.
Câu 3. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$, có bảng biến thiên như hình sau:
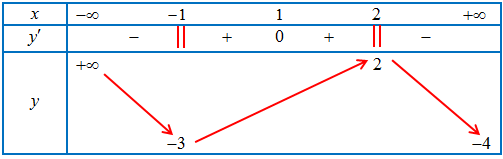
Khi đó:
a) Hàm số có hai điểm cực trị.
b) Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3 .
c) Hàm số đạt cực đại tại $x = 2$
d) Hàm số nghịch biến trên mỗi khoảng $\left( { – \infty ; – 1} \right),\left( {2; + \infty } \right)$.
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Đúng |
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.
Câu 4. Cho hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$, khi đó:
a) Hàm số đồng biến trên khoảng $\left( {1;37} \right)$.
b) Hàm số có 3 điểm cực trị.
c) Giá trị nhỏ nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 12.
d) Giá trị lớn nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 33.
Lời giải
| a) Sai | b) Đúng | c) Sai | d) Đúng |
Bảng biến thiên của hàm số
$f(x) = – {x^4} + 12{x^2} + 1$ liên tục trên $[ – 1;2]$.
$f'(x) = – 4{x^3} + 24{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \sqrt 6 \,\,(loại)} \\
{x = – \sqrt 6 \,\,(loại)}
\end{array}} \right.$
Ta có:
$f\left( { – 1} \right) = 12;f\left( 2 \right) = 33;f\left( 0 \right) = 1$
Giá trị lớn nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 33 tại $x = 2$
Giá trị nhỏ nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 1 tại $x = 0$
Câu 5. Cho hàm số $f\left( x \right) = {x^3} – 24x$, khi đó:
a) Hàm số nghịch biến trên khoảng $\left( { – \infty ;0} \right)$
b) Đồ thị hàm số có điểm cực tiểu là $A\left( {16; – 2048} \right)$
c) Giá trị lớn nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng 6403 .
d) Giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng -40 .
Lời giải
| a) Sai | b) Đúng | c) Đúng | d) Sai |
Bảng biến thiên của hàm số
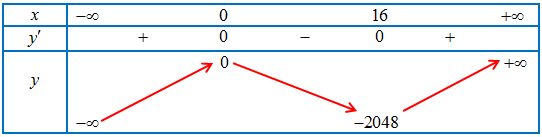
Ta có $f’\left( x \right) = 3{x^2} – 24 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2\sqrt 2 \in \left[ {2;19} \right]} \\
{x = – 2\sqrt 2 \notin \left[ {2;19} \right]}
\end{array}} \right.$.
$f\left( 2 \right) = {2^3} – 24.2 = – 40$; $f\left( {2\sqrt 2 } \right) = {(2\sqrt 2 )^3} – 24.2\sqrt 2 = – 32\sqrt 2 $; $f\left( {19} \right) = {19^3} – 24.19 = 6403$.
Vậy giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng $ – 32\sqrt 2 $.
Câu 6. Cho hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$. Khi đó
a) Hàm số nghịch biến trên khoảng $\left( {0;6} \right)$
b) Hàm số có 3 điểm cực trị
c) Giá trị lớn nhất của hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$ trên $\left[ {0;9} \right]$ bằng-4.
d) Giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$ trên $\left[ {0;9} \right]$ bằng -29 .
Lời giải
| a) Sai | b) Đúng | c) Sai | d) Đúng |
Bảng biến thiên của hàm số
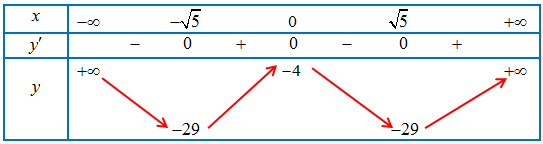Hàm số $y = f\left( x \right)$ liên tục trên $\left[ {0;9} \right]$.
Có $f’\left( x \right) = 4{x^3} – 20x$,
$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \sqrt 5 } \\
{x = – \sqrt 5 \notin \left[ {0;9} \right]}
\end{array}} \right.$
Ta có $f\left( 0 \right) = – 4$, $f\left( {\sqrt 5 } \right) = – 29$, $f\left( 9 \right) = 5747$
Câu 7. Cho hàm số $y = x + \frac{4}{x}$ trên khoảng $\left( {0; + \infty } \right)$. Khi đó:
a) Hàm số nghịch biến trên khoảng $\left( {0;2} \right)$
b) Hàm số có 1 điểm cực trị.
c) Hàm số đạt giá trị lớn nhất tại $x = 3$
d) Giá trị nhỏ nhất của hàm số bằng 4
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Đúng |
Hàm số $y = x + \frac{4}{x}$ liên tục và xác định trên $\left( {0; + \infty } \right)$.
Ta có $y’ = 1 – \frac{4}{{{x^2}}} = \frac{{{x^2} – 4}}{{{x^2}}} \Rightarrow $$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2 \in \left( {0; + \infty } \right)} \\
{x = – 2 \notin \left( {0; + \infty } \right)}
\end{array}} \right.$.
Bảng biến thiên
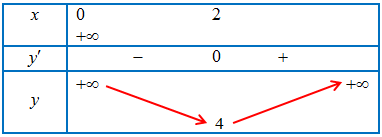
Vậy giá trị nhỏ nhất là $m = 4$ khi $x = 2$.
Hàm số không có giá trị lớn nhất.
Câu 8. Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$, đồ thị của hàm số $y = f’\left( x \right)$ như hình vẽ.
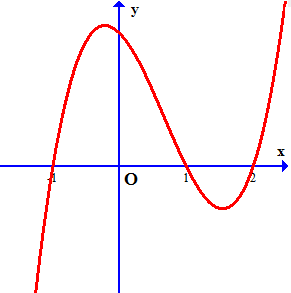
Khi đó:
a) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị
b) Hàm số $y = f\left( x \right)$ nghịch biến trên khoảng $\left( {1;2} \right)$
c) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {2; + \infty } \right)$
d) Giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ { – 1;2} \right]$ là $f\left( 2 \right)$
Lời giải
| a) Sai | b) Đúng | c) Đúng | d) Sai |
$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = – 1} \\
{x = 1} \\
{x = 2}
\end{array}} \right.$
Từ đồ thị hàm $y = f’\left( x \right)$ ta có bảng biến thiên
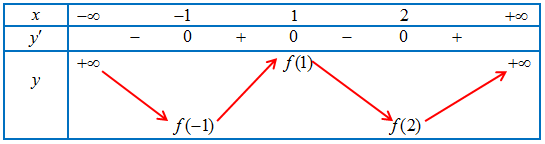
Từ đó suy ra giá trị lớn nhất của hàm số trên $\left[ { – 1;2} \right]$ là $f\left( 1 \right)$.
Câu 9. Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $R$. Hàm số $y = f’\left( x \right)$ có đồ thị như hình sau:
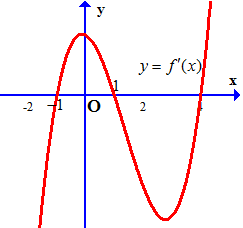
Khi đó:
a) Hàm số $y = f\left( x \right)$ có hai cực trị
b) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {1; + \infty } \right)$
c) $f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)$.
d) Trên đoạn $\left[ { – 1;4} \right]$, giá trị lớn nhất của hàm số $y = f\left( x \right)$ là $f\left( 1 \right)$.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Đúng |
Dựa vào đồ thị của hàm số $y = f’\left( x \right)$ ta thấy:
$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1} \\
{x = 1} \\
{x = 4}
\end{array}} \right.$
$f’\left( x \right) < 0 \Leftrightarrow x \in \left( { – \infty ; – 1} \right) \cup \left( {1;4} \right)$
$f’\left( x \right) > 0 \Leftrightarrow x \in \left( { – 1;1} \right) \cup \left( {4; + \infty } \right)$
Ta có bảng biến thiên của hàm số $y = f\left( x \right)$
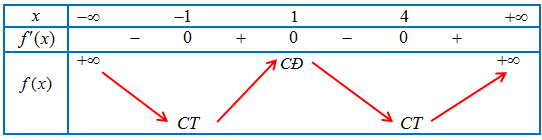
Dựa vào bảng biến thiên đáp án đúng là mệnh đề c và d
Câu 10. Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {0;\frac{7}{2}} \right]$ có đồ thị hàm số $y = f’\left( x \right)$ như hình vẽ.
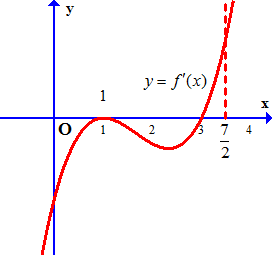
a) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {3;\frac{7}{2}} \right)$
b) $f\left( 0 \right) > f\left( 3 \right)$
c) $f\left( 3 \right) > f\left( {\frac{7}{2}} \right)$
d) Hàm số $y = f\left( x \right)$ đạt giá trị nhỏ nhất trên đoạn $\left[ {0;\frac{7}{2}} \right]$ tại điểm ${x_0} = \frac{7}{2}$
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
Dựa vào đồ thị hàm số $y = f’\left( x \right)$ ta có bảng biến thiên trên đoạn $\left[ {0;\frac{7}{2}} \right]$ như sau:
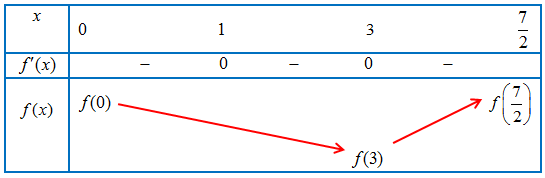
Do đó hàm số đạt giá trị nhỏ nhất tại ${x_0} = 3$.
Câu 11. Cho hàm số $y = \frac{{x – {m^2} – 2}}{{x – m}}$, (tham số $m$ ). Khi đó:
a) Tập xác định: $D = \mathbb{R}$.
b) Khi $m = 1$ hàm số đồng biến trên mỗi khoảng $\left( { – \infty ;1} \right)$ và $\left( {1; + \infty } \right)$.
c) Khi $m = 1$ thì trên đoạn $\left[ {1;4} \right]$ hàm số đạt giá trị lớn nhất bằng $\frac{1}{2}$
d) Có 1 giá trị của tham số $m$ để giá trị lớn nhất của hàm số $y = \frac{{x – {m^2} – 2}}{{x – m}}$ trên đoạn $\left[ {0;4} \right]$ bằng -1 .
Lời giải
| a) Sai | b) Đúng | c) Sai | d) Đúng |
Tập xác định: $D = \mathbb{R} \setminus \left\{ m \right\}$.
$y’ = \frac{{{m^2} – m + 2}}{{{{(x – m)}^2}}} > 0,\forall x \ne m$. Do đó hàm số đồng biến trên mỗi khoảng $\left( { – \infty ;m} \right)$ và $\left( {m; + \infty } \right)$.
Bảng biến thiên của hàm số:
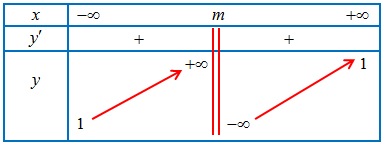
Từ bảng biến thiên suy ra, hàm số đạt giá trị lớn nhất trên đoạn $\left[ {0;4} \right]$ bằng -1 khi $\left\{ \begin{gathered}
\left[ {0;4} \right] \subset D \hfill \\
\mathop {\max y}\limits_{\left[ {0;4} \right]} = f(4) = – 1 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{\frac{{2 – {m^2}}}{{4 – m}} = – 1}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{{m^2} + m – 6 = 0}
\end{array}} \right.} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{m = 2,m = – 3}
\end{array} \Leftrightarrow m = – 3} \right.$.
Câu 12. Cho hàm số $y = \frac{{{x^2} + mx + 1}}{{x + m}}$ (tham số $m$ ). Khi đó:
a) Khi $m = 1$ hàm số có 2 điểm cực trị
b) Khi $m = 1$ hàm số đồng biến trên khoảng $\left( {0; + \infty } \right)$
c) Để hàm số liên tục trên $\left[ {0;2} \right]$ thì $\left[ {\begin{array}{*{20}{l}}
{m > 0} \\
{m < – 2}
\end{array}} \right.$
d) Để hàm số $y = \frac{{{x^2} + mx + 1}}{{x + m}}$ liên tục và đạt giá trị nhỏ nhất trên đoạn $\left[ {0;2} \right]$ tại một điểm ${x_0} \in \left( {0;2} \right)$ thì $m > 1$
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
Tập xác định: $D = \mathbb{R} \setminus \left\{ { – m} \right\}$. Hàm số liên tục trên $\left[ {0;2} \right] \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{ – m < 0} \\
{ – m > 2}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m > 0} \\
{m < – 2}
\end{array}} \right.} \right.$
Ta có $y’ = \frac{{{x^2} + 2mx + {m^2} – 1}}{{{{(x + m)}^2}}} = \frac{{{{(x + m)}^2} – 1}}{{{{(x + m)}^2}}}$.
Cho $y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x_1} = – m – 1} \\
{{x_2} = – m + 1}
\end{array}} \right.$.
Ta có bảng biến thiên
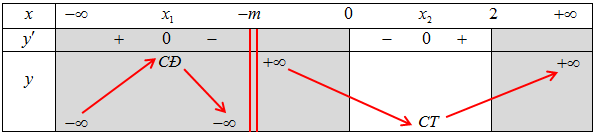
Hàm số đạt giá trị nhỏ nhất tại ${x_0} \in \left( {0;2} \right)$ nên $0 < – m + 1 < 2 \Leftrightarrow – 1 < m < 1$
So với điều kiện hàm số liên tục trên đoạn $\left[ {0;2} \right]$.
Ta có $0 < m < 1$.
Câu 13. Cho hàm số $y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 2025$, (tham số $m$ ). Khi đó:
a) Khi $m = 1$ thì hàm số đạt cực tiểu tại $x = 2$
b) Khi $m = 1$ thì hàm số đồng biến trên khoảng $\left( {0;2} \right)$
c) Khi $m = 1$ thì hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ bằng -4
d) Có tất cả 1 giá trị nguyên của $m$ để hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
Ta có: $y’ = 3{x^2} – 6mx + 3\left( {{m^2} – 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x_1} = m – 1} \\
{{x_2} = m + 1}
\end{array}} \right.$.
Để hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ thì ${x_1} \leqslant 0 < {x_2}$ hoặc $0 < {x_1} < {x_2}$.
TH1: ${x_1} \leqslant 0 < {x_2} \Leftrightarrow m – 1 \leqslant 0 < m + 1 \Leftrightarrow – 1 < m \leqslant 1$. Do $m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1} \right\}$.
BBT của hàm số:
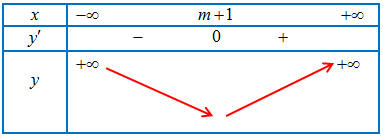
TH2: $0 < {x_1} < {x_2}$.
BBT của hàm số
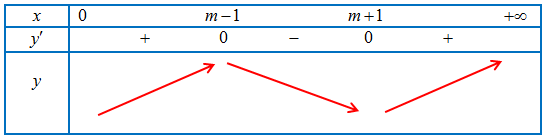
Hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ khi và chỉ khi $\left\{ {\begin{array}{*{20}{l}}
{m – 1 > 0} \\
{y\left( {m + 1} \right) \leqslant y\left( 0 \right)}
\end{array}} \right.$.
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{{{(m + 1)}^3} – 3m{{(m + 1)}^2} + 3\left( {{m^2} – 1} \right)\left( {m + 1} \right) + 2025 \leqslant 2025}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{{{(m + 1)}^2}\left( {m – 2} \right) \leqslant 0}
\end{array}} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{\left[ \begin{gathered}
m \leqslant 2 \hfill \\
m = – 1 \hfill \\
\end{gathered} \right.}
\end{array}} \right.$$ \Leftrightarrow 1 < m \leqslant 2$.
Do $m \in \mathbb{Z} \Rightarrow m = 2$.
Vậy $m \in \left\{ {0;1;2} \right\}$.
Câu 14. Cho hàm số $y = f\left( x \right) = {x^3} – 3x + m + 1$, (tham số $m$ ). Khi đó:
a) Khi $m = 0$ thì hàm số $y = – f\left( x \right)$ có 2 điểm cực trị
b) Khi $m = 0$ thì hàm số $y = f\left( x \right)$ nghịch biến trên khoảng $\left( {1; + \infty } \right)$
c) Khi $m = 0$ thì hàm số $y = – f\left( x \right)$ đạt giá trị lớn nhất trên khoảng $\left( { – 1; + \infty } \right)$ tại $x = 1$
d) Tổng tất cả các giá trị của tham số $m$ sao cho giá trị nhỏ nhất của hàm số $y = {[f\left( x \right)]^2}$ trên đoạn $\left[ { – 1;1} \right]$ bằng 1 là -2
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
Bảng biến thiên của $g\left( x \right)$
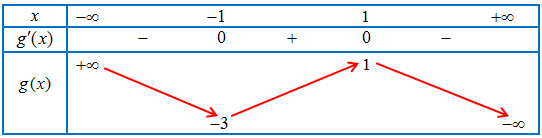
d) Đặt $y = f\left( x \right) = {\left( {{x^3} – 3x + m + 1} \right)^2}$ là hàm số xác định và liên tục trên đoạn $\left[ { – 1;1} \right]$.
Ta có $y’ = f’\left( x \right) = 2\left( {{x^3} – 3x + m + 1} \right)\left( {3{x^2} – 3} \right)$.
$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pm 1} \\
{m = – {x^3} + 3x – 1 = g\left( x \right)}
\end{array}} \right.$.
Ta khảo sát hàm số $g\left( x \right)$ trên đoạn $\left[ { – 1;1} \right]$.
Bảng biến thiên của $g\left( x \right)$
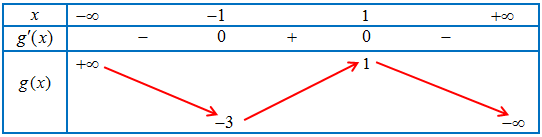
Nếu $m \in \left[ { – 3;1} \right]$ thì luôn tồn tại ${x_0} \in \left[ { – 1;1} \right]$ sao cho $m = g\left( {{x_0}} \right)$ hay $f\left( {{x_0}} \right) = 0$. Suy ra $\mathop {min}\limits_{\left[ { – 1;1} \right]} y = 0$, tức là không tồn tại $m$. thỏa mãn yêu cầu bài toán.
Nếu $m \notin \left[ { – 3;1} \right]$ thì $f’\left( x \right) = 0 \Leftrightarrow x = \pm 1 \in \left[ { – 1;1} \right]$.
Ta có: $\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = min\left\{ {f\left( 1 \right);f\left( { – 1} \right)} \right\} = min\left\{ {{{(m – 1)}^2};{{(m + 3)}^2}} \right\}$
Trường hợp 1: $m > 1$ tức là $m + 3 > m – 1 > 0$ suy ra
$\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = {\left( {m – 1} \right)^2} = 1$$ \Leftrightarrow \left[ \begin{gathered}
m = 2\,(TM) \hfill \\
m = 0\,(KTM) \hfill \\
\end{gathered} \right.$
Trường hợp 2: $m < – 3$ tức là $m – 1 < m + 3 < 0$ suy ra
$\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = {(m + 3)^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = – 4\left( {TM} \right)} \\
{m = – 2\left( {KTM} \right)}
\end{array}} \right.$
Vậy có hai giá trị của $m$ thỏa mãn yêu cầu bài toán: $m = 2;m = – 4$, từ đó tổng tất cả các giá trị của $m$ là -2 .
Câu 15. Cho hàm số $f\left( x \right) = m{x^4} + 2\left( {m – 1} \right){x^2}$ với $m$ là tham số thực. Khi đó:
a) Khi $m = 1$ hàm số có 3 điểm cực trị
b) Khi $m = 0$ hàm số có 3 điểm cực trị
c) Khi $m = \frac{1}{2}$ thì giá trị nhỏ nhất của hàm số bằng $ – \frac{1}{2}$
d) Nếu thì bằng 3
Lời giải
a) Sai b) Đúng c) Đúng d) Sai
$f’\left( x \right) = 4m{x^3} + 4\left( {m – 1} \right)x$.
Do $f\left( x \right)$ là hàm đa thức và
$ \Leftrightarrow 4m + 4\left( {m – 1} \right) = 0 \Rightarrow m = \frac{1}{2}$.
Thay $m = \frac{1}{2}$ vào hàm số ban đầu ta được
$y = \frac{1}{2}{x^4} + 2\left( {\frac{1}{2} – 1} \right){x^2} = \frac{1}{2}{x^4} – {x^2}$
$ \Rightarrow y’ = 2{x^3} – 2x = 2x\left( {x – 1} \right)\left( {x + 1} \right)$
Ta có BBT:
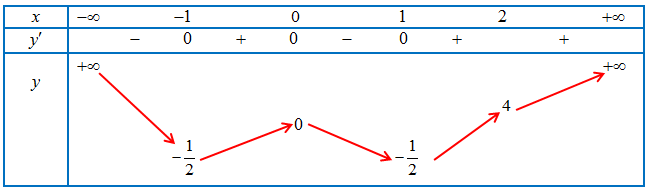
Vậy với $m = \frac{1}{2}$, thì $\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right)\left( {TM} \right)$.
Dựa vào BBT ta có .
Câu 16. Cho hàm số $f\left( x \right)$, đồ thị hàm số $y = f’\left( x \right)$ là đường cong trong hình bên.
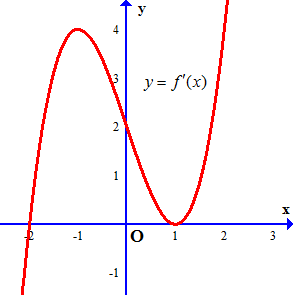
a) Hàm số $f\left( x \right)$ đồng biến trên khoảng $\left( {1; + \infty } \right)$ và $\left( { – \infty ; – 2} \right)$
b) Hàm số $f\left( x \right)$ có 2 điểm cực trị
c) Hàm số $g\left( x \right) = f\left( {\frac{x}{2}} \right)$ nghịch biến trên khoảng $\left( { – 5; – 4} \right)$
d) Giá trị nhỏ nhất của hàm số $g\left( x \right) = f\left( {\frac{x}{2}} \right)$ trên đoạn $\left[ { – 5;3} \right]$ bằng $f\left( { – 2} \right)$
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Đúng |
${g^\prime }(x) = 0 \Leftrightarrow \frac{1}{2}{f^\prime }\left( {\frac{x}{2}} \right) = 0$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\frac{x}{2} = – 2} \\
{\frac{x}{2} = 1}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 4} \\
{x = 2}
\end{array} } \right.} \right.$.
${g^\prime }(x) < 0 \Leftrightarrow {f^\prime }\left( {\frac{x}{2}} \right) < 0 \Leftrightarrow \frac{x}{2} < – 2 \Leftrightarrow x < – 4$
Bảng biến thiên
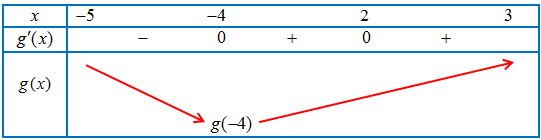
Giá trị nhỏ nhất của hàm số $g\left( x \right)$ trên $\left[ { – 5;3} \right]$ bằng $g\left( { – 4} \right) = f\left( { – 2} \right)$.
Câu 17. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình dưới đây.
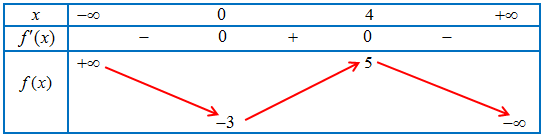
a) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị
b) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( { – 3;5} \right)$
c) Giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ {1;3} \right]$ bằng $f\left( 1 \right)$
d) Giá trị lớn nhất của hàm số $g\left( x \right) = f\left( {4x – {x^2}} \right) + \frac{1}{3}{x^3} – 3{x^2} + 8x + \frac{1}{3}$ trên đoạn $\left[ {1;3} \right]$ bằng 12
Lời giải
| a) Đúng | b) Sai | c) Sai | d) Đúng |
$g’\left( x \right) = \left( {4 – 2x} \right)f’\left( {4x – {x^2}} \right) + {x^2} – 6x + 8$
$ = \left( {2 – x} \right)\left[ {2f’\left( {4x – {x^2}} \right) + 4 – x} \right]$.
Với $x \in \left[ {1;3} \right]$ thì $4 – x > 0;3 \leqslant 4x – {x^2} \leqslant 4$ nên $f’\left( {4x – {x^2}} \right) > 0$.
Suy ra $2f’\left( {4x – {x^2}} \right) + 4 – x > 0,\forall x \in \left[ {1;3} \right]$.
Bảng biến thiên
Suy ra $\mathop {max}\limits_{\left[ {1;3} \right]} g\left( x \right) = g\left( 2 \right) = f\left( 4 \right) + 7 = 12$.
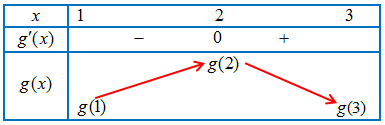
Câu 18. Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và $f\left( 0 \right) \geqslant – 1$. Đồ thị của hàm số $y = f’\left( x \right)$ như hình vẽ.
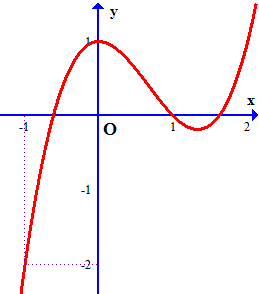
a) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {0;1} \right)$
b) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị
c) Hàm số $y = f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2$ có 3 điểm cực trị
d) Hàm số $y = \left| {f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2} \right|$ có giá trị nhỏ nhất là $m \in \left( {0;1} \right)$ khi và chỉ khi $ – \frac{4}{3} < f\left( 2 \right) < \frac{1}{3}$
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Đúng |
Xét $g\left( x \right) = f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2$
$ \Rightarrow g’\left( x \right) = f’\left( x \right) – {x^2} + 2x – 1$;
$g’\left( x \right) = 0 \Leftrightarrow f’\left( x \right) = {x^2} – 2x + 1$.
Vẽ $\left( P \right):y = {x^2} – 2x + 1$ cắt $y = f’\left( x \right)$ tai ba điểm có hoành độ $x = 0;x = 1;x = 2$.
Ta có bảng biến thiên của $y = g\left( x \right)$ như sau
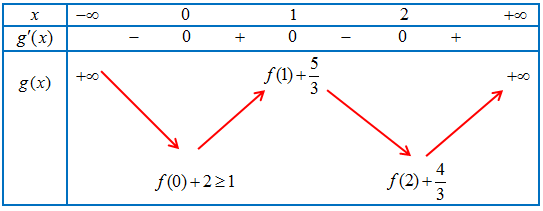
Từ bảng biến thiên ta thấy:
Nếu $f\left( 2 \right) + \frac{4}{3} < 0 \Rightarrow \left| {g\left( x \right)} \right| \geqslant 0 \Rightarrow Min\left| {g\left( x \right)} \right| = 0$.
Do đó để $min\left| {g\left( x \right)} \right| = m \in \left( {0;1} \right)$$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( 2 \right) + \frac{4}{3} > 0} \\
{f\left( 2 \right) + \frac{4}{3} < 1}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( 2 \right) > \frac{{ – 4}}{3}} \\
{f\left( 2 \right) < – \frac{1}{3}}
\end{array}} \right.$.
Vậy $ – \frac{4}{3} < f\left( 2 \right) < \frac{1}{3}$
Câu 19. Cho hàm số $y = f\left( x \right) = {x^3} – 3x + m$ (tham số thực $m$ ). Khi đó:
a) Khi $m = 0$ thì hàm số đồng biến trên khoảng $\left( { – 1;1} \right)$
b) Khi $m = 0$ thì hàm số có 2 điểm cực trị
c) Hàm số có giá trị nhỏ nhất trên đoạn $\left[ {0;2} \right]$ bằng $m – 2$
d) Gọi $S$ là tập hợp tất cả các giá trị của tham số thực $m$ sao cho giá trị lớn nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên đoạn $\left[ {0;2} \right]$ bằng 3 . Số phần tử của $S$ là 1
Lời giải
| a) Sai | b) Đúng | c) Đúng | d) Sai |
d) Xét hàm số $f\left( x \right) = {x^3} – 3x + m$, ta có $f’\left( x \right) = 3{x^2} – 3$. Ta có bảng biến thiên của $f\left( x \right)$ :
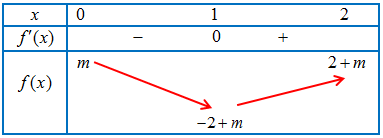
Cách 1. Dựa vào bảng biến thiên ta suy ra, $H = \mathop {max}\limits_{\left[ {0;2} \right]} f\left( x \right) = 2 + m$ và $K = \mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = – 2 + m$
Vậy, $\mathop {max}\limits_{\left[ {0;2} \right]} |f(x)| = \frac{{|H + K| + |H – K|}}{2}$
$ = \frac{{|(2 + m) + ( – 2 + m)| + |(2 + m) – ( – 2 + m)|}}{2} = \frac{{|2m| + 4}}{2}$
Theo đề cho $\mathop {max}\limits_{\left[ {0;2} \right]} |f(x)| = 3 \Leftrightarrow \frac{{|2m| + 4}}{2} = 3$
$ \Leftrightarrow |2m| = 2 \Leftrightarrow \left[ \begin{gathered}
2m = 2 \hfill \\
2m = – 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m = 1 \hfill \\
m = – 1 \hfill \\
\end{gathered} \right.$
Vậy, số phần tử của $S$ là $2$.
Chú ý: Để tìm Giá trị lớn nhất và nhỏ nhất của hàm số $y = \left| {f(x)} \right|$ ta làm như sau:
Bước 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$.
Giả sử $\mathop {\min }\limits_D f(x) = m$; $\mathop {\max }\limits_D f(x) = M$.
Bước 2: $\mathop {max}\limits_D |f(x)| = \frac{{|M + m| + |M – m|}}{2}$;
$\mathop {\min }\limits_D |f(x)| = \left\{ {\begin{array}{*{20}{l}}
{\frac{{|M + m| – |M – m|}}{2}}&{ khi\,\, m.M \geqslant 0} \\
0&{ khi \,\,m.M < 0}
\end{array}} \right.$.
Cách 2. Dựa vào bảng biến thiên ta phân thành các trường hợp sau
TH 1 : $2 + m < 0 \Leftrightarrow m < – 2$. Khi đó $\mathop {max}\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = – \left( { – 2 + m} \right) = 2 – m$
$2 – m = 3 \Leftrightarrow m = – 1$ (loại).
TH 2: $\left\{ {\begin{array}{*{20}{l}}
{2 + m > 0} \\
{m < 0}
\end{array} \Leftrightarrow – 2 < m < 0} \right.$. Khi đó : $\;\left| {m – 2} \right| = 2 – m > 2 > 2 + m$
$2 – m = 3 \Leftrightarrow m = – 1$ (thỏa mãn).
TH 3: $\left\{ {\begin{array}{*{20}{l}}
{m > 0} \\
{ – 2 + m < 0}
\end{array} \Leftrightarrow 0 < m < 2} \right.$. Khi đó : $2 + m = 3 \Leftrightarrow m = 1$ (thỏa mãn).
TH 4: $ – 2 + m > 0 \Leftrightarrow m > 2$. Khi đó
$2 + m = 3 \Leftrightarrow m = 1$ (loại).
Vậy, số phần tử của $S$ là $2$.
Câu 20. Cho hàm số $y = {x^4} – 2{x^2} + 3m$ với $m$ là tham số. Khi đó :
a) Hàm số đồng biến trên khoảng $\left( {1; + \infty } \right)$
b) Hàm số có 3 điểm cực trị
c) Giá trị nhỏ nhất của hàm số trên đoạn $\left[ { – 1;2} \right]$ là $3m + 1$
d) Biết rằng có đúng hai giá trị ${m_1},{m_2}$ của $m$ để giá trị nhỏ nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên $\left[ { – 1;2} \right]$ bằng $2025$. Khi đó giá trị $\left| {{m_1} – {m_2}} \right|$ bằng $\frac{8}{3}$
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
d) Xét hàm số $f\left( x \right) = {x^4} – 2{x^2} + 3m$, ta có
$f’\left( x \right) = 4{x^3} – 4x = 4x\left( {{x^2} – 1} \right)f’\left( x \right) = 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \pm 1}
\end{array}} \right.$
Bảng biến thiên của hàm số trên $\left[ { – 1;2} \right]$ :
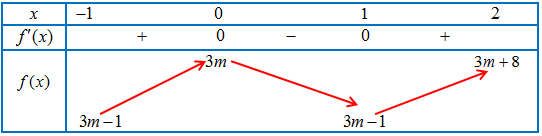
Suy ra, $H = \mathop {max}\limits_{\left[ { – 1;2} \right]} f(x) = 3m + 8$; $K = \mathop {\min }\limits_{\left[ { – 1;2} \right]} f(x) = 3m – 1$
TH1: $H.K \geqslant 0 \Leftrightarrow \left( {3m + 8} \right)\left( {3m – 1} \right) \geqslant 0 \Leftrightarrow \left[ \begin{gathered}
m \leqslant – \frac{8}{3} \hfill \\
m \geqslant \frac{1}{3} \hfill \\
\end{gathered} \right.$
Ta có: $\mathop {\min }\limits_{\left[ { – 1;2} \right]} \left| {f\left( x \right)} \right| = \frac{{\left| {(3m + 8) + (3m – 1)} \right| – \left| {(3m + 8) – (3m – 1)} \right|}}{2}$
$ = \frac{{\left| {6m + 7} \right| – 9}}{2} = 2025$
$\frac{{\left| {6m + 7} \right| – 9}}{2} = 2025$
$ \Leftrightarrow \left| {6m + 7} \right| = 4059 \Leftrightarrow \left[ \begin{gathered}
6m + 7 = 4059 \hfill \\
6m + 7 = – 4059 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
m = \frac{{2026}}{3}\,(nhan) \hfill \\
m = – \frac{{2033}}{3}\,(nhan) \hfill \\
\end{gathered} \right.$
Khi đó giá trị $\left| {{m_1} – {m_2}} \right| = \left| {\frac{{2026}}{3} – \left( { – \frac{{2033}}{3}} \right)} \right| = 1353$
TH2: $H.K < 0 \Leftrightarrow \left( {3m + 8} \right)\left( {3m – 1} \right) < 0$ $ \Leftrightarrow – \frac{8}{3} < m < \frac{1}{3}$
$\mathop {\min }\limits_{\left[ { – 1;2} \right]} \left| {f\left( x \right)} \right| = 0$ (loại)
Vậy, $\left| {{m_1} – {m_2}} \right| = \left| {\frac{{2026}}{3} – \left( { – \frac{{2033}}{3}} \right)} \right| = 1353$. Do đó d) sai.
———-
Để lại một bình luận