Phương Pháp Tìm m Để Hàm Số Đạt Cực Trị Tại Một Điểm – Tài Liệu Toán

I. Phương pháp

Bước 1. Tính $y’\left( {{x_0}} \right)$

Bước 2. Giải phương trình $y’\left( {{x_0}} \right) = 0 \Rightarrow m$ ?

Bước 3. Thay $m$ vào thử lại bằng cách lập bảng biến thiên.

II. Các ví dụ minh họa

Ví dụ 1. Tìm $m$ để hàm số $y = – {x^3} – 2m{x^2} + 2mx + 5$ đạt cực đại tại $x = 2$.

Lời giải

$y = – 3{x^2} – 4mx + 2m$

Để $x = 2$ là điểm cực đại của hàm số thì $y’\left( 2 \right) = 0$$ \Leftrightarrow – 12 – 8m + 2m = 0 \Leftrightarrow m = – 2$.

Thử lại với $m = – 2$, ta có $y = – {x^3} + 4{x^2} – 4x + 5$;

$y’ = – 3{x^2} + 8x – 4$

$y’ = 0 \Leftrightarrow – 3{x^2} + 8x – 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2} \\
{x = \frac{2}{3}}
\end{array}} \right.$

Bảng biến thiên:

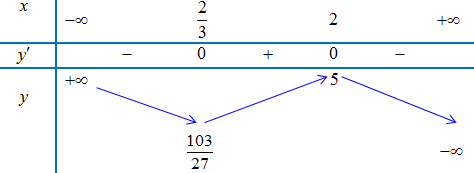
Vậy $m = – 2$ thỏa yêu cầu bài toán.

Ví dụ 2. Tìm $m$ để hàm số $y = – {x^3} + 4m{x^2} + mx + {m^2}$ đạt cực tiểu tại $x = 1$

Lời giải

Để $x = 1$ là điểm cực tiểu của hàm số thì $y’\left( 1 \right) = 0 \Leftrightarrow 3 – 4m + m = 0 \Leftrightarrow m = 1$.

Thử lại với $m = 1$, ta có $y = {x^3} – 2{x^2} + x + 1$; $y’ = 3{x^2} – 4x + 1$

$y’ = 0 \Leftrightarrow 3{x^2} – 4x + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1} \\
{x = \frac{1}{3}}
\end{array}} \right.$

Bảng biến thiên:

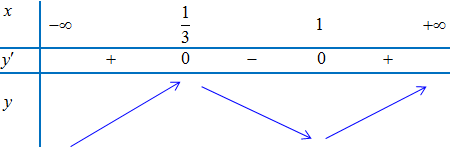
Dựa vào bảng biến thiên ta thấy $m = 1$ thỏa yêu cầu bài toán.

Ví dụ 3. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \frac{1}{3}{x^3} – m{x^2} + \left( {m + 1} \right)x – 1$ đạt cực tiểu tại $x = – 2$

Lời giải

Ta có $y’ = {x^2} – 2mx + m + 1$.

Để $x = – 2$ là điểm cực tiểu của hàm số đã cho thì $y’\left( { – 2} \right) = 0 \Leftrightarrow {( – 2)^2} – 2m\left( { – 2} \right) + m + 1 = 0 \Leftrightarrow 5m + 5 = 0 \Leftrightarrow m = – 1$.

Với $m = – 1$, ta có $y = \frac{1}{3}{x^3} + {x^2} – 1$.

$y’ = {x^2} + 2x$;

$y’ = 0 \Leftrightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 2} \\
{x = 0}
\end{array}} \right.$

Ta có bảng biến thiên:

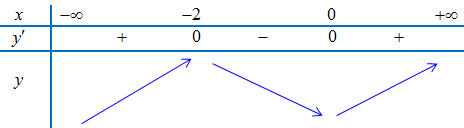
Dựa vào bảng biến thiên, ta thấy $m = – 1$ không thỏa yêu cầu bài toán.

Vậy không có giá trị nào của $m$ thỏa yêu cầu bài toán.

Ví dụ 4. Tìm tất cả tham số thực $m$ để hàm số $y = \left( {m – 1} \right){x^4} – \left( {{m^2} – 2} \right){x^2} + 2025$ đạt cực tiểu tại $x = – 1$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Đạo hàm: $y’ = 4\left( {m – 1} \right){x^3} – 2\left( {{m^2} – 2} \right)x$.

Hàm số đạt cực tiểu tại $x = – 1 \Rightarrow y’\left( { – 1} \right) = 0 \Leftrightarrow – 4\left( {m – 1} \right) + 2\left( {{m^2} – 2} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = 0} \\
{m = 2}
\end{array}} \right.$.

Với $m = 0$, hàm số trở thành $y = – {x^4} + 2{x^2} + 2025$.

$y’ = – 4{x^3} + 4x$; $y’ = 0 \Leftrightarrow – 4{x^3} + 4x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = 0 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên:

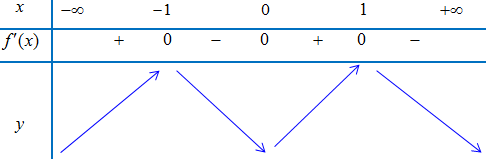
Suy ra, hàm số đạt cực đại tại $x = – 1$ nên $m = 0$ không thỏa yêu cầu bài toán.

Với $m = 2$, hàm số trở thành $y = {x^4} – 2{x^2} + 2025$.

$y’ = 4{x^3} – 4x$; $y’ = 0 \Leftrightarrow 4{x^3} – 4x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = 0 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$

Bảng biến thiên:

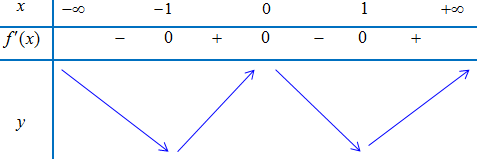
Suy ra, hàm số đạt cực tiểu tại $x = – 1$ nên $m = 2$ thỏa yêu cầu bài toán.

Vậy $m = 2$ thì hàm số $y = \left( {m – 1} \right){x^4} – \left( {{m^2} – 2} \right){x^2} + 2025$ đạt cực tiểu tại $x = – 1$.

———-