Phương Pháp Xét Tính Đơn Điệu Của Hàm Số Cho Bởi Công Thức – Tài Liệu Toán

Phương pháp xét tính đơn điệu của hàm số cho bởi công thức: Hàm bậc hai, bậc ba, trùng phương; Hàm phân thức hữu tỉ; hàm chứa căn bậc hai.

I. Phương pháp

Bước 1: Tìm tập xác định $D$.

Bước 2: Tính đạo hàm $y’ = f’\left( x \right)$.

Bước 3: Tìm nghiệm của $f’\left( x \right)$ hoặc những giá trị $x$ làm cho $f’\left( x \right)$ không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

II. Các ví dụ minh họa

Ví dụ 1. Xét tính đơn điệu của hàm số $y = {x^2} + 4x – 2$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 2x + 4$;

$y’ = 0 \Leftrightarrow $ $2x + 4 = 0 \Leftrightarrow x = – 2$

Bảng biến thiên

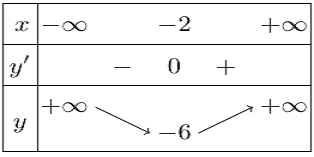
Vậy hàm số đồng biến trên khoảng $\left( { – 2; + \infty } \right)$, nghịch biến trên khoảng $\left( { – \infty ; – 2} \right)$

Ví dụ 2. Tìm các khoảng đồng biến, nghịch biến của hàm số $y = {x^3} – 3{x^2} + 1$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 3{x^2} – 6x;y’ = 0$

$ \Leftrightarrow 3{x^2} – 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = 2}
\end{array}} \right.$.

Bảng biến thiên

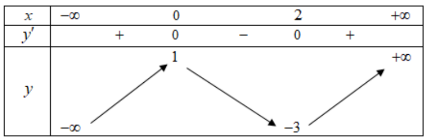
Vậy hàm số đồng biến trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {2; + \infty } \right)$, nghịch biến trên khoảng $\left( {0;2} \right)$.

Ví dụ 3. Xét tính đơn điệu của hàm số $y = – {x^3} + 3{x^2} – 3x$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = – 3{x^2} + 6x – 3$;

$y’ = 0$ $ \Leftrightarrow – 3{x^2} + 6x – 3 = 0 \Leftrightarrow x = 1$ (nghiệm kép)

Bảng biến thiên

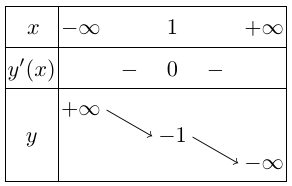
Vậy hàm số nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.

Ví dụ 4. Tìm các khoảng đơn điệu của hàm số $y = {x^4} – 2{x^2}$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có $y’ = 4{x^3} – 4x = 4x\left( {{x^2} – 1} \right);$

$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \pm 1}
\end{array}} \right.$.

Bảng biến thiên:

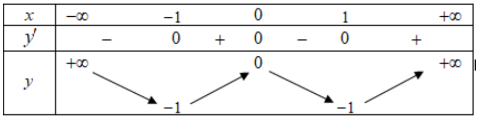
Vậy hàm số đồng biến trên các khoảng $\left( { – 1;0} \right)$ và $\left( {1; + \infty } \right)$, nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {0;1} \right)$.

Ví dụ 5. Tìm các khoảng đơn điệu của hàm số $y = \frac{{x + 4}}{{x + 3}}$.

Lời giải

Tập xác định: $D = \mathbb{R} \setminus \left\{ { – 3} \right\}$.

Ta có $y’ = \frac{{1 \cdot 3 – 4 \cdot 1}}{{{{(x + 3)}^2}}} = \frac{1}{{{{(x + 3)}^2}}} < 0,\forall x \in D$.

Vậy hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 3} \right)$ và $\left( { – 3; + \infty } \right)$.

Ví dụ 6. Tìm các khoảng đơn điệu của hàm số $y = \frac{{3x + 1}}{{1 – x}}$.

Lời giải

$y = \frac{{3x + 1}}{{ – x + 1}}$

Tập xác định: $D = \mathbb{R} \setminus \left\{ 1 \right\}$.

Ta có $y’ = \frac{{3 \cdot 1 – \left( { – 1} \right) \cdot 1}}{{{{(1 – x)}^2}}} = \frac{4}{{{{(1 – x)}^2}}} > 0,\forall x \in D$.

Vậy hàm số đồng biến trên các khoảng $\left( { – \infty ;1} \right)$ và $\left( {1; + \infty } \right)$.

Ví dụ 7. Tìm các khoảng nghịch biến của hàm số: $y = \frac{{{x^2} – 3x + 4}}{{x – 3}}$.

Lời giải

Tập xác định: $D = \mathbb{R} \setminus \left\{ 3 \right\}$.

Ta có: $y’ = \frac{{{{\left( {{x^2} – 3x + 4} \right)}^\prime }\left( {x – 3} \right) – \left( {{x^2} – 3x + 4} \right){{\left( {x – 3} \right)}^\prime }}}{{{{\left( {x – 3} \right)}^2}}}$

$ = \frac{{\left( {2x – 3} \right)\left( {x – 3} \right) – \left( {{x^2} – 3x + 4} \right).1}}{{{{\left( {x – 3} \right)}^2}}}$

$ = \frac{{2{x^2} – 6x – 3x + 9 – {x^2} + 3x – 4}}{{{{\left( {x – 3} \right)}^2}}}$ $ = \frac{{{x^2} – 6x + 5}}{{{{\left( {x – 3} \right)}^2}}}$.

$y’ = 0 \Leftrightarrow \frac{{{x^2} – 6x + 5}}{{{{\left( {x – 3} \right)}^2}}} = 0$$ \Leftrightarrow {x^2} – 6x + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 5} \\
{x = 1}
\end{array}} \right.$

Bảng biến thiên

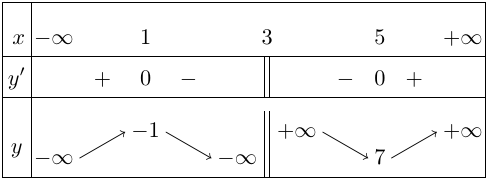
Vậy hàm số đồng biến trên các khoảng $\left( { – \infty ;1} \right)$ và $\left( {5; + \infty } \right)$, nghịch biến trên các khoảng $\left( {1;3} \right)$ và $\left( {3;5} \right)$.

Ví dụ 8. Tìm các khoảng nghịch biến của hàm số: $y = \frac{{ – {x^2} + 2x – 1}}{{x + 2}}$.

Lời giải

Tập xác định: $D = \mathbb{R} \setminus \left\{ { – 2} \right\}$.

Ta có: $y’ = \frac{{ – {x^2} – 4x + 5}}{{{{(x + 2)}^2}}}$.

$y’ = 0 \Leftrightarrow \frac{{ – {x^2} – 4x + 5}}{{{{(x + 2)}^2}}} = 0$$ \Leftrightarrow – {x^2} – 4x + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 5} \\
{x = 1}
\end{array}} \right.$

Bảng biến thiên

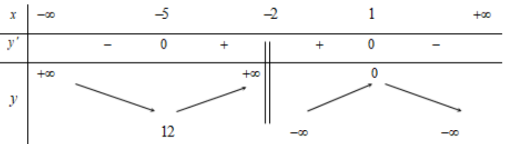
Vậy hàm số đồng biến trên các khoảng $\left( { – 5; – 2} \right)$ và $\left( { – 2;1} \right)$, nghịch biến trên các khoảng $\left( { – \infty ; – 5} \right)$ và $\left( {1; + \infty } \right)$.

Ví dụ 9. Tìm các khoảng đơn điệu của hàm số $y = \sqrt {{x^2} – 4x + 3} $.

Lời giải

Tập xác định $D = \left( { – \infty ;1} \right] \cup \left[ {3; + \infty } \right)$.

$y’ = \frac{{{{\left( {{x^2} – 4x + 3} \right)}^\prime }}}{{2\sqrt {{x^2} – 4x + 3} }} = \frac{{2x – 4}}{{2\sqrt {{x^2} – 4x + 3} }}$

$y’ = 0 \Rightarrow 2x – 4 = 0 \Rightarrow x = 2$ (loại)

Bảng biến thiên

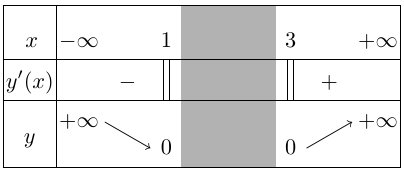
Suy ra hàm số đồng biến trên khoảng $\left( {3; + \infty } \right)$, nghịch biến trên các khoảng $\left( { – \infty ;1} \right)$.

Ví dụ 10. Tìm các khoảng đơn điệu của hàm số $y = x\sqrt {4 – {x^2}} $.

Lời giải

Tập xác định $D = \left[ { – 2;2} \right]$.

$y’ = \sqrt {4 – {x^2}} – \frac{{{x^2}}}{{\sqrt {4 – {x^2}} }} = \frac{{4 – 2{x^2}}}{{\sqrt {4 – {x^2}} }};y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – \sqrt 2 } \\
{x = \sqrt 2 }
\end{array}} \right.$

Bảng biến thiên

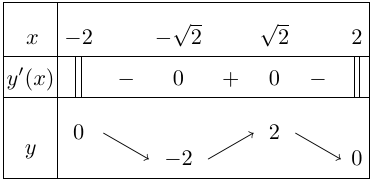
Suy ra hàm số đồng biến trên khoảng $\left( { – \sqrt 2 ;\sqrt 2 } \right)$, nghịch biến trên các khoảng $\left( { – 2; – \sqrt 2 } \right)$ và $\left( {\sqrt 2 ;2} \right)$.

———-