20 câu hỏi trả lời ngắn tiệm cận của đồ thị hàm số giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Câu 1: Tiệm cận ngang của đồ thị hàm số $y = \frac{{10x}}{{2x – 1}}$ là:
Lời giải
Trả lời: $5$
Ta có : $\mathop {\lim }\limits_{x \to + \infty } y = \frac{{10}}{2} = 5$ và $\mathop {\lim }\limits_{x \to – \infty } y = \frac{{10}}{2} = 5$ nên $y = 5$ là tiệm cận ngang của đồ thị hàm số.
Câu 2: Tiệm cận đứng của đồ thị hàm số $y = \frac{{5 + x}}{{x – 3}}$ là
Lời giải
Trả lời: $3$
Tập xác định $D = \mathbb{R}\backslash \{ 3\} $.
Ta có $\mathop {\lim }\limits_{x \to {3^ – }} y = – \infty $; $\mathop {\lim }\limits_{x \to {3^ + }} y = + \infty $ suy ra đồ thị có tiệm cận đứng là $x = 3$
Câu 3: Tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} – 4x + 5}}{{x – 4}}$ là.
Lời giải
Trả lời: $y = x$
$y = \frac{{{x^2} – 4x + 5}}{{x – 4}} = x + \frac{5}{{x – 4}}$
$ \Rightarrow $TCX: $y = x$
Câu 4: Với giá trị nào của tham số $m$ thì đường tiệm cận ngang của đồ thị hàm số $y = \frac{{mx + 3}}{{2x – 2025}}$ đi qua điểm $M(1;3)$?
Lời giải
Trả lời: $6$
Ta có $\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{m + \frac{3}{x}}}{{2 – \frac{{2025}}{x}}} = \frac{m}{2}\, \Rightarrow $Tiệm cận ngang $y = \frac{m}{2}$
Vì tiệm cận ngang đi qua điểm $M(1;3)$nên $3 = \frac{m}{2} \Leftrightarrow m = 6$
Câu 5: Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
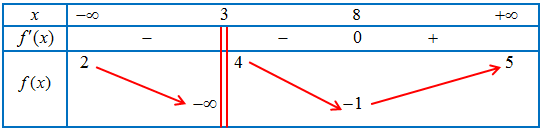
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho:
Lời giải
Trả lời: $3$
* Tìm tiệm cận đứng
Hàm số không xác định tại ${x_0} = 3$.
Ta có:
$\mathop {\lim }\limits_{x \to {3^ + }} y = 4$; $\mathop {\lim }\limits_{x \to {3^ – }} y = – \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 3$
* Tìm tiệm cận ngang
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = 5$; $\mathop {\lim }\limits_{x \to – \infty } y = 2$
$ \Rightarrow $Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 20$ và $y = 2$
Vậy hàm số có 3 tiệm cận
Câu 6: Cho hàm số $f\left( x \right)$ có bảng biến thiền như sau
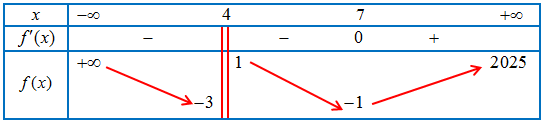
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là.
Lời giải
Trả lời: $1$
* Tìm tiệm cận đứng
Hàm số không xác định tại ${x_0} = 4$.
Ta có:
$\mathop {\lim }\limits_{x \to {4^ + }} y = 1$; $\mathop {\lim }\limits_{x \to {4^ – }} y = – 3$
$ \Rightarrow $$x = 4$ không phải là tiệm cận đứng của đồ thị hàm số.
* Tìm tiệm cận ngang
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = 2025$; $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 2025$.
Vậy hàm số có $1$ tiệm cận.
Câu 7: Cho hàm số $y = f\left( x \right)$có bảng biến thiên như sau
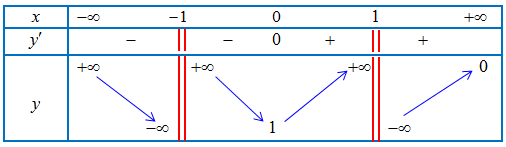
Tính tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Lời giải
Ta có: $\mathop {\lim }\limits_{x \to + \infty } y = 0 \Rightarrow y = 0$ là tiệm cận ngang của đồ thị hàm số
$\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty \Rightarrow x = – 1$ là tiệm cận đứng của đồ thị hàm số
$\mathop {\lim }\limits_{x \to {1^ – }} y = + \infty \Rightarrow x = 1$ là tiệm cận đứng của đồ thị hàm số
Đồ thị hàm số có 3 đường tiệm cận.
Câu 8: Số tiệm cận đứng của đồ thị hàm số $y = \frac{{\sqrt {x + 16} – 4}}{{{x^2} + x}}$ là
Lời giải
Trả lời: 1
Tập xác định của hàm số: $D = \left[ { – 16; + \infty } \right)\backslash \left\{ {0; – 1} \right\}$
Ta có:
* $\mathop {\lim }\limits_{x \to – {1^ – }} y = – \infty $; $\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – 1$
* $\mathop {\lim }\limits_{x \to {0^ – }} y = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{\sqrt {x + 16} – 4}}{{{x^2} + x}}$
$ = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{\left( {\sqrt {x + 16} – 4} \right)\left( {\sqrt {x + 16} + 4} \right)}}{{\left( {{x^2} + x} \right)\left( {\sqrt {x + 16} + 4} \right)}}$$ = \mathop {\lim }\limits_{x \to {0^ – }} \frac{x}{{\left( {{x^2} + x} \right)\left( {\sqrt {x + 16} + 4} \right)}}$
$ = \mathop {\lim }\limits_{x \to {0^ – }} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt {x + 16} + 4} \right)}} = \frac{1}{{\left( {0 + 1} \right)\left( {\sqrt {0 + 16} + 4} \right)}} = \frac{1}{8}$;
Tương tự $\mathop {\lim }\limits_{x \to – {1^ + }} y = \frac{1}{8}$
$ \Rightarrow x = 0$ không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có 1 tiệm cận đứng.
Câu 9: Đồ thị hàm số $f\left( x \right) = \frac{{2 – x}}{{\sqrt {{x^2} – 4} }}$ có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?
Lời giải
Trả lời: 1 TCĐ, 2 TCN
Tập xác định của hàm số $D = \left( { – \infty ; – 2} \right) \cup \left( {2; + \infty } \right)$.
* Tìm tiệm cận đứng
+ $\mathop {\lim }\limits_{x \to – {2^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to – {2^ – }} \frac{{2 – x}}{{\sqrt {{x^2} – 4} }} = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – 2$
+ $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{2 – x}}{{\sqrt {{x^2} – 4} }} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{ – {{\left( {\sqrt {x – 2} } \right)}^2}}}{{\sqrt {x – 2} .\sqrt {x + 2} }} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{ – \sqrt {x – 2} }}{{\sqrt {x + 2} }} = 0$
$ \Rightarrow x = 2$ không là đường tiệm cận đứng của đồ thị hàm số.
* Tìm tiệm cận ngang
Ta có:
+ $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 – x}}{{\sqrt {{x^2} – 4} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{2}{x} – 1} \right)}}{{\left| x \right|\sqrt {1 – \frac{4}{{{x^2}}}} }}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{2}{x} – 1} \right)}}{{x\sqrt {1 – \frac{4}{{{x^2}}}} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {\frac{2}{x} – 1} \right)}}{{\sqrt {1 – \frac{4}{{{x^2}}}} }} = – 1$;
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = – 1$.
+ $\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } \frac{{2 – x}}{{\sqrt {{x^2} – 4} }} = \mathop {\lim }\limits_{x \to – \infty } \frac{{x\left( {\frac{2}{x} – 1} \right)}}{{\left| x \right|\sqrt {1 – \frac{4}{{{x^2}}}} }}$
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{x\left( {\frac{2}{x} – 1} \right)}}{{ – x\sqrt {1 – \frac{4}{{{x^2}}}} }} = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left( {\frac{2}{x} – 1} \right)}}{{ – \sqrt {1 – \frac{4}{{{x^2}}}} }} = 1$;
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 1$.
Vậy hàm số 2 TCN và 1 TCĐ
Câu 10: Đồ thị hàm số $y = \frac{{1 – \sqrt {4 – {x^2}} }}{{{x^2} – 2x – 3}}$ có số đường tiệm cận đứng là $m$ và số đường tiệm cận ngang là $n$. Tính giá trị của $m + n$.
Lời giải
Trả lời: 1
$D = \left[ { – 2;2} \right] \setminus \left\{ { – 1} \right\}$
$\mathop {\lim }\limits_{x \to {{( – 1)}^ + }} y = \mathop {\lim }\limits_{x \to {{( – 1)}^ + }} \frac{{1 – \sqrt {4 – {x^2}} }}{{{x^2} – 2x – 3}} = + \infty $;
$\mathop {\lim }\limits_{x \to {{( – 1)}^ – }} y = \mathop {\lim }\limits_{x \to {{( – 1)}^ – }} \frac{{1 – \sqrt {4 – {x^2}} }}{{{x^2} – 2x – 3}} = – \infty $
$ \Rightarrow x = – 1$ là tiệm cận đứng.
Đồ thị hàm số không có đường tiệm cận ngang.
Vậy $m + n = 1$.
Câu 11: Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y = mx + \sqrt {{x^2} + x + 1} $ có tiệm cận ngang?
Lời giải
Trả lời: $2$
Nếu $m > 0$ thì đồ thị hàm số tiệm cận ngang khi $x \to – \infty $ và $\mathop {\lim }\limits_{x \to – \infty } \left( {mx + \sqrt {{x^2} + x + 1} } \right)$ hữu hạn.
Xét: $\mathop {\lim }\limits_{x \to – \infty } \left( {mx + \sqrt {{x^2} + x + 1} } \right) = \mathop {\lim }\limits_{x \to – \infty } \left( {\frac{{\left( {{m^2} – 1} \right){x^2} – x – 1}}{{mx – \sqrt {{x^2} + x + 1} }}} \right)$
Giới hạn có kết quả hữu hạn khi: ${m^2} – 1 = 0 \Leftrightarrow m = 1{\text{ }}\left( {m > 0} \right)$
Nếu $m < 0$ thì đồ thị hàm số tiệm cận ngang khi $x \to + \infty $ và $\mathop {\lim }\limits_{x \to + \infty } \left( {mx + \sqrt {{x^2} + x + 1} } \right)$ hữu hạn.
Xét: $\mathop {\lim }\limits_{x \to + \infty } \left( {mx + \sqrt {{x^2} + x + 1} } \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{\left( {{m^2} – 1} \right){x^2} – x – 1}}{{mx – \sqrt {{x^2} + x + 1} }}} \right)$
Giới hạn có kết quả hữu hạn khi: ${m^2} – 1 = 0 \Leftrightarrow m = – 1{\text{ }}\left( {m < 0} \right)$
Vậy có $2$ giá trị nguyên của tham số $m$ để đồ thị hàm số có tiệm cận ngang.
Câu 12: Gọi $S$ là tập hợp các giá trị nguyên $m$ để đồ thị hàm số $y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} – 6x + 2m} }}$ có hai đường tiệm cận đứng. Số phần tử của $S$ là.
Lời giải
Trả lời: 12
Điều kiện xác định $\left\{ {\begin{array}{*{20}{l}}
{x + 2 \geqslant 0} \\
{{x^2} – 6x + 2m > 0}
\end{array}} \right.$.
Để đồ thị hàm số có hai đường tiệm cận đứng thì phương trình ${x^2} – 6x + 2m = 0$ có hai nghiệm phân biệt ${x_1},{x_2}$ lớn hơn $ – 2$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{\Delta ^\prime } = 9 – 2m > 0} \\
{{x_1} + {x_2} > – 2} \\
{{{( – 2)}^2} – 6 \cdot ( – 2) + 2m > 0}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < \frac{9}{2}} \\
{3 > – 2} \\
{4 + 12 + 2m > 0}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < \frac{9}{2}} \\
{m > – 8}
\end{array}} \right.$
Do đó tập $S = \left\{ { – 7; – 6; – 5; \ldots ;4} \right\}$ có 12 giá trị.
Câu 13: Gọi $S$ là tập hợp tất cả các giá trị của tham số thực $m$ sao cho đồ thị hàm số $f\left( x \right) = \frac{x}{{\sqrt {{x^3} + mx + 1} – \sqrt[3]{{{x^4} + x + 1}} + {m^2}x}}$ nhận trục tung làm tiệm cận đứng. Tính tổng các phần tử của $S$.
Lời giải
Trả lời: $ – \frac{1}{2}$
Ta có: $\mathop {\lim }\limits_{x \to 0} f(x) = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\frac{{\sqrt {{x^3} + mx + 1} – \sqrt[3]{{{x^4} + x + 1}} + {m^2}x}}{x}}}$.
Mà $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^3} + mx + 1} – \sqrt[3]{{{x^4} + x + 1}} + {m^2}x}}{{{\text{ x }}}}$
$ = \mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sqrt {{x^3} + mx + 1} – 1}}{x} – \frac{{\sqrt[3]{{{x^4} + x + 1}} – 1}}{x} + \frac{{{m^2}x}}{x}} \right]$
$ = \mathop {\lim }\limits_{x \to 0} \left[ {\frac{{{x^3} + mx}}{{x\left( {\sqrt {{x^3} + mx + 1} + 1} \right)}} – \frac{{{x^4} + x}}{{x\left( {\sqrt[3]{{{{\left( {{x^4} + x + 1} \right)}^2}}} + \sqrt[3]{{{x^4} + x + 1}} + 1} \right)}} + {m^2}} \right]$
$ = \mathop {\lim }\limits_{x \to 0} \left[ {\frac{{{x^2} + m}}{{\left( {\sqrt {{x^3} + mx + 1} + 1} \right)}} – \frac{{{x^3} + 1}}{{\left( {\sqrt[3]{{{{\left( {{x^4} + x + 1} \right)}^2}}} + \sqrt[3]{{{x^4} + x + 1}} + 1} \right)}} + {m^2}} \right]$
$ = \frac{m}{2} – \frac{1}{2} + {m^2} = {m^2} + \frac{m}{2} – \frac{1}{2}$
Đồ thị hàm số $f(x)$ nhận trục tung làm tiệm cận đứng
$ \Leftrightarrow \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\left( {{x^2} + m} \right)}}{{\left( {\sqrt {{x^3} + mx + 1} + 1} \right)}} – \frac{{\left( {{x^3} + 1} \right)}}{{\sqrt[3]{{{{\left( {{x^4} + x + 1} \right)}^2}}} + \sqrt[3]{{{x^4} + x + 1}} + 1}} + {m^2}} \right) = 0$
$ \Leftrightarrow {m^2} + \frac{m}{2} – \frac{1}{2} = 0$$ \Leftrightarrow 6{m^2} + 3m – 2 = 0$
$ \Rightarrow {m_1} + {m_2} = \frac{{ – b}}{a} = \frac{{ – 3}}{6} = – \frac{1}{2}.$
Câu 14: Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ:
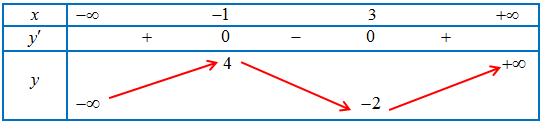
Số đường tiệm cận đứng của đồ thị hàm số $y = \frac{{2025}}{{f\left( x \right)}}$ là
Lời giải
Trả lời: $3$
Từ bảng biến thiên ta thấy $f\left( x \right) = 0$ có 3 nghiệm ${x_1},{x_2},{x_3}$ phân biệt.
Do vậy $\mathop {\lim }\limits_{x \to {x_1}} y = \pm \infty ;\mathop {\lim }\limits_{x \to {x_2}} y = \pm \infty ;\mathop {\lim }\limits_{x \to {x_3}} y = \pm \infty $ nên đồ thị hàm số $y = \frac{{2025}}{{f\left( x \right)}}$ có 3 đường tiệm cận đứng.
Câu 15: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây.
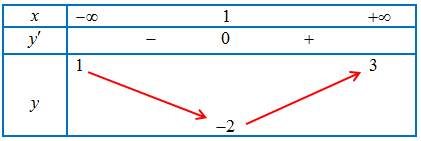
Tổng số đường tiệm cận của hàm số $y = \frac{1}{{f\left( x \right) + 1}}$ là:
Lời giải
Trả lời: 4
Số đường tiệm cận đứng của đồ thị là số nghiệm của phương trình $f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = – 1$.
Từ bảng biến thiên ta thấy phương trình có hai nghiệm phân biệt nên đồ thị hàm số $y = \frac{1}{{f\left( x \right) + 1}}$ có hai đường tiệm cận đứng.
Ta có$\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f(x) + 1}} = \frac{1}{{3 + 1}} = \frac{1}{4}$; $\mathop {\lim }\limits_{x \to – \infty } \frac{1}{{f(x) + 1}} = \frac{1}{{1 + 1}} = \frac{1}{2}$ nên đồ thị hàm số có hai đường tiệm cận ngang là $y = \frac{1}{4}$ và $y = \frac{1}{2}$.
Vậy đồ thị hàm số $y = \frac{1}{{f\left( x \right) + 1}}$ có bốn đường tiệm cận.
Câu 16: Cho hàm số $y = f\left( x \right)$ xác định, liề tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ bên dưới.
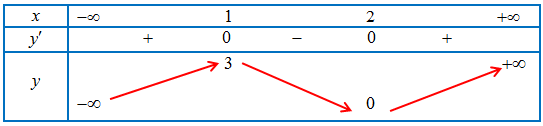
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1}{{f\left( {{x^3} + x} \right) + 3}}$ là:
Lời giải
Trả lời: 4
Đặt $t = {x^3} + x$, ta có khi $x \to – \infty $ thì $t \to – \infty $ và khi $x \to + \infty $ thì $t \to + \infty $.
Mặt khác ta có $t’ = 3{x^2} + 1 > 0,\forall x \in \mathbb{R}$ nên với mọi $t \in \mathbb{R}$ phương trình ${x^3} + x = t$ có duy nhất một nghiệm $x$.
Số đường tiệm cận đứng của đồ thị là số nghiệm của phương trình
$f\left( t \right) + 3 = 0 \Leftrightarrow f\left( t \right) = – 3$
Từ bảng biến thiên ta thấy phương trình có duy nhất một nghiệm nên đồ thị hàm số $y = \frac{1}{{f\left( {{x^3} + x} \right) + 3}}$ có một tiệm cận đứng.
Ta có $\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{f\left( {{x^3} + x} \right) + 3}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{{f(t) + 3}} = 0$;
$\mathop {\lim }\limits_{x \to – \infty } \frac{1}{{f\left( {{x^3} + x} \right) + 3}} = \mathop {\lim }\limits_{t \to – \infty } \frac{1}{{f(t) + 3}} = 0$
nên đồ thị hàm số $y = \frac{1}{{f\left( {{x^3} + x} \right) + 3}}$ có một tiệm cận ngang là $y = 0$.
Vậy đồ thị có hai đường tiệm cận
Câu 17: Cho hàm số bậc ba $f\left( x \right) = a{x^3} + b{x^2} + cx + d\left( {a,b,c,d \in \mathbb{R}} \right)$ có đồ thị như hình vẽ dưới đây.
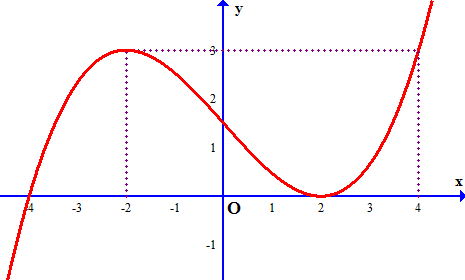
Đồ thị hàm số $g\left( x \right) = \frac{1}{{f\left( {4 – {x^2}} \right) – 3}}$ có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Lời giải
Trả lời: 4
Đặt $t = 4 – {x^2}$, ta có khi $x \to \pm \infty $ thì $t \to – \infty $.
Khi đó $\mathop {\lim }\limits_{x \to \pm \infty } g(x) = \mathop {\lim }\limits_{t \to – \infty } \frac{1}{{f(t) – 3}} = 0$ nên $y = 0$ là tiệm cận ngang của đồ thị hàm số $g(x)$.
Mặt khác $f\left( {4 – {x^2}} \right) – 3 = 0 \Leftrightarrow f\left( {4 – {x^2}} \right) = 3$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{4 – {x^2} = – 2} \\
{4 – {x^2} = 4}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pm \sqrt 6 } \\
{x = 0}
\end{array}} \right.} \right.$
$ \Rightarrow $ Đồ thị hàm số $g\left( x \right)$ có ba đương tiệm cận đứng
Vậy đồ thị hàm số $g\left( x \right)$ có bốn đường tiệm cận.
Câu 18: Cho đồ thị hàm số $y = a{x^3} + b{x^2} + cx + d$ như hình vẽ dưới đây:
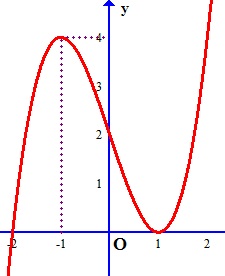
Đồ thị của hàm số $g\left( x \right) = \frac{{3{x^2} – x – 2}}{{3{f^2}\left( x \right) – 6f\left( x \right)}}$ có bao nhiêu đường tiện cận đứng?
Lời giải
Trả lời: 5
Xét phương trình $3{f^2}\left( x \right) – 6f\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{f\left( x \right) = 0} \\
{f\left( x \right) = 2}
\end{array}} \right.$
Dựa vào đồ thị ta suy ra:
Phương trình $f\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 2} \\
{x = 1}
\end{array}} \right.$, với $x = – 2$ là nghiệm đơn và $x = 1$ là nghiệm kép.
Suy ra: $f\left( x \right) = a\left( {x + 2} \right){(x – 1)^2},\left( {a \ne 0} \right)$.
Phương trình $f\left( x \right) = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = m\,( – 2 < m < – 1),\;\;} \\
{x = n(n > 1)}
\end{array}} \right.$
Suy ra $f\left( x \right) – 2 = ax\left( {x – m} \right)\left( {x – n} \right),\left( {a \ne 0} \right)$.
Khi đó: $g\left( x \right) = \frac{{{a^2}\left( {x – 1} \right)\left( {3x + 2} \right)}}{{3f\left( x \right)\left[ {f\left( x \right) – 2} \right]}}$$ = \frac{{\left( {x – 1} \right)\left( {3x + 2} \right)}}{{3{a^2}\left( {x + 2} \right){{(x – 1)}^2}x\left( {x – m} \right)\left( {x – n} \right)}}$
$ = \frac{{\left( {3x + 2} \right)}}{{3{a^2}x\left( {x + 2} \right)\left( {x – 1} \right)\left( {x – m} \right)\left( {x – n} \right)}},\left( {a \ne 0} \right)$
Vậy đồ thị hàm số $g\left( x \right)$ có 5 đường tiệm cận đứng
Cách 2: Chọn hàm số $f\left( x \right)$.
Ta có $f\left( x \right) = a{x^3} + b{x^2} + cx + d$
Đồ thị hàm số qua 4 điểm $A\left( { – 2;0} \right),B\left( { – 1;4} \right)$, $C\left( {0;2} \right),D\left( {1;0} \right)$.
suy ra $\left\{ {\begin{array}{*{20}{l}}
{a = 1} \\
{b = 0} \\
{c = – 3} \\
{d = 2}
\end{array}} \right.$ hay $f\left( x \right) = {x^3} – 3x + 2$
Khi đó:
$g\left( x \right) = \frac{{3{x^2} – x – 2}}{{3{f^2}\left( x \right) – 6f\left( x \right)}}$$ = \frac{{3{x^2} – x – 2}}{{3f\left( x \right)\left( {f\left( x \right) – 2} \right)}}$
$ = \frac{{3{x^2} – x – 2}}{{3\left( {{x^3} – 3x + 2} \right)\left( {{x^3} – 3x} \right)}}$$ = \frac{{\left( {x – 1} \right)\left( {3x + 2} \right)}}{{3\left( {x + 2} \right){{(x – 1)}^2}x\left( {{x^2} – 3} \right)}}$
Vậy đồ thị hàm số $g\left( x \right)$ có 5 đường tiệm cận đứng
Câu 19: Cho hàm số bậc ba $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới.
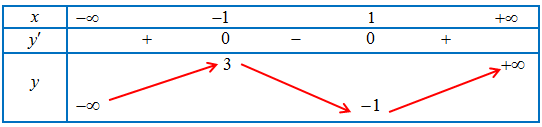
Đồ thị hàm số $g\left( x \right) = \frac{{2x + 7 – 3\sqrt {4x + 5} }}{{\left| {f\left( x \right)} \right| – 1}}$ có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang
Lời giải
Trả lời: 2
Hàm số $g\left( x \right)$ xác định khi $\left\{ \begin{gathered}
x \geqslant – \frac{5}{4} \hfill \\
f(x) \ne \pm 1 \hfill \\
\end{gathered} \right.$
Ta có $y = f\left( x \right)$ là hàm bậc ba và dựa vảo bảng biến thiên ta có $y’ = a\left( {{x^2} – 1} \right)$
$ \Rightarrow y = \frac{a}{3}{x^3} – ax + b$.
$\left\{ {\begin{array}{*{20}{l}}
{y\left( { – 1} \right) = 3} \\
{y\left( 1 \right) = – 1}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – \frac{a}{3} + a + b = 3} \\
{\frac{a}{3} – a + b = – 1\;}
\end{array}} \right.} \right.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 3} \\
{b = 1}
\end{array} \Rightarrow y = {x^3} – 3x + 1} \right.$
$\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 7 – 3\sqrt {4x + 5} }}{{\left| {{x^3} – 3x + 1} \right| – 1}}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{2}{{{x^2}}} + \frac{7}{{{x^3}}} – 3\sqrt {\frac{4}{{{x^5}}} + \frac{5}{{{x^6}}}} }}{{\left| {1 – \frac{3}{{{x^2}}} + \frac{1}{{{x^3}}}} \right| – \frac{1}{{{x^3}}}}} = 0$
$ \Rightarrow y = 0$ là tiệm cận ngang của đồ thị hàm số.
$g\left( x \right) = \frac{{2x + 7 – 3\sqrt {4x + 5} }}{{\left| {f\left( x \right)} \right| – 1}}$
$ = \frac{{\left( {4{x^2} – 8x + 4} \right)\left( {\left| {f\left( x \right)} \right| + 1} \right)}}{{\left( {{f^2}\left( x \right) – 1} \right)\left( {2x + 7 + 3\sqrt {4x + 5} } \right)}}$
$ = \frac{{4{{(x – 1)}^2}\left( {\left| {f\left( x \right)} \right| + 1} \right)}}{{\left( {f\left( x \right) – 1} \right)\left( {f\left( x \right) + 1} \right)\left( {2x + 7 + 3\sqrt {4x + 5} } \right)}}$
$ = \frac{{4{{(x – 1)}^2}\left( {\left| {f\left( x \right)} \right| + 1} \right)}}{{x\left( {x + \sqrt 3 } \right)\left( {x – \sqrt 3 } \right)\left( {x + 2} \right){{(x – 1)}^2}\left( {2x + 7 + 3\sqrt {4x + 5} } \right)}}$
$ = \frac{{4\left( {\left| {f\left( x \right)} \right| + 1} \right)}}{{x\left( {x + \sqrt 3 } \right)\left( {x – \sqrt 3 } \right)\left( {x + 2} \right)\left( {2x + 7 + 3\sqrt {4x + 5} } \right)}}$
$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {0^ + }} g(x) = – \infty } \\
{\mathop {\lim }\limits_{x \to {0^ – }} g(x) = + \infty }
\end{array} \Rightarrow x = 0} \right.$ là tiệm cận đứng của đồ thị hàm số.
$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {{\sqrt 3 }^ + }} g(x) = + \infty } \\
{\mathop {\lim }\limits_{x \to {{\sqrt 3 }^ – }} g(x) = – \infty }
\end{array} \Rightarrow x = \sqrt 3 } \right.$ là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tiện cận ngang là $y = 0$ và tiệm cận đứng là $y = \sqrt 3 $
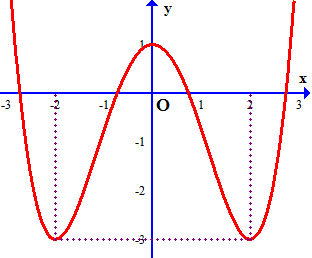
Câu 20: Cho hàm trùng phương $y = a{x^4} + b{x^2} + c$ có đồ thị như hình vẽ. Hỏi đồ thị hàm số $y = \frac{{\left( {{x^2} – 4} \right)\left( {{x^2} + 2x} \right)}}{{{{[f\left( x \right)]}^2} + 2f\left( x \right) – 3}}$ có tổng cộng bao nhiêu tiệm cận đứng?
Lời giải
Trả lời : 4
Ta có: $y = \frac{{\left( {{x^2} – 4} \right)\left( {{x^2} + 2x} \right)}}{{{{[f\left( x \right)]}^2} + 2f\left( x \right) – 3}}$$ = \frac{{\left( {x – 2} \right)\left( {x + 2} \right)x\left( {x + 2} \right)}}{{{{[f\left( x \right)]}^2} + 2f\left( x \right) – 3}}$
$ = \frac{{\left( {x – 2} \right){{(x + 2)}^2}x}}{{{{[f\left( x \right)]}^2} + 2f\left( x \right) – 3}}$.
Xét ${[f\left( x \right)]^2} + 2f\left( x \right) – 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{\;f(x) = 1\;} \\
{f\left( x \right) = – 3}
\end{array}} \right.$
$ \Leftrightarrow \left[ \begin{gathered}
x = m,m < – 2 \hfill \\
x = 0 \hfill \\
x = n,\,n > 2 \hfill \\
x = 2 \hfill \\
x = – 2 \hfill \\
\end{gathered} \right.$.
Dựa vào đồ thị ta thấy các nghiệm $x = 0;x = \pm 2$ là các nghiệm kép (nghiệm bội 2 ).
Do đó đa thức ${[f\left( x \right)]^2} + 2f\left( x \right) – 3$ có bậc là 8 .
Suy ra $y = \frac{{\left( {x – 2} \right){{(x + 2)}^2}x}}{{{a^2}{x^2}{{(x + 2)}^2}{{(x – 2)}^2}\left( {x – m} \right)\left( {x – n} \right)}}$
$ = \frac{1}{{{a^2}x\left( {x – 2} \right)\left( {x – m} \right)\left( {x – n} \right)}}$.
Vậy đồ thị hàm số có 4 đường tiệm cận đứng là $x = 0,x = 2,x = m,x = n$.
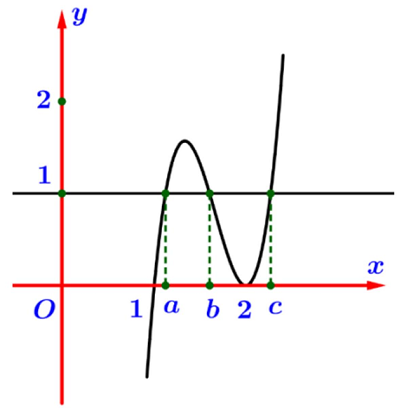
Câu 21: Cho hàm số bậc ba $f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ. Hỏi đồ thị hàm số $g\left( x \right) = \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x\left[ {{f^2}\left( x \right) – f\left( x \right)} \right]}}$ có bao nhiêu đường tiệm cận?
Lời giải
Trả lời: 6
Điều kiện xác định của hàm số $g\left( x \right)$ là $x \geqslant 1$.
Xét phương trình $x\left[ {{f^2}\left( x \right) – f\left( x \right)} \right] = 0$$ \Leftrightarrow x.f\left( x \right) \cdot \left[ {f\left( x \right) – 1} \right] = 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{f\left( x \right) = 0.} \\
{f\left( x \right) = 1}
\end{array}} \right.$
Xét phương trình $f\left( x \right) = 0$ có nghiệm kép $x = 2$ và nghiệm đơn $x = 1$.
Xét phương trình $f\left( x \right) = 1$ có ba nghiệm đơn $\left[ {\begin{array}{*{20}{l}}
{x = a,1 < a < 2} \\
{x = b,1 < b < 2,b \ne a} \\
{x = c,c > 2}
\end{array}} \right.$. Ta thấy $\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty } \\
{\mathop {\lim }\limits_{x \to – \infty } f(x) = – \infty }
\end{array}} \right.$
Nên không mất tính tổng quát, ta có
$ + f\left( x \right) = 0 \Leftrightarrow \left( {x – 1} \right){(x – 2)^2} = 0$
$ + f\left( x \right) = 1 \Leftrightarrow \left( {x – a} \right)\left( {x – b} \right)\left( {x – c} \right) = 0$
Do đó:
$g\left( x \right) = \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x\left[ {{f^2}\left( x \right) – f\left( x \right)} \right]}} = \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x\left( {x – 1} \right){{(x – 2)}^2}\left( {x – a} \right)\left( {x – b} \right)\left( {x – c} \right)}}$
Khi đó
+$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {0^ + }} g(x)} \\
{\mathop {\lim }\limits_{x \to {0^ – }} g(x)}
\end{array}} \right.$.
không tồn tại giới hạn $ \Rightarrow x = 0$ không là tiệm cận đứng của đồ thị hàm số $g\left( x \right)$
$ + \mathop {\lim }\limits_{x \to {1^ + }} g(x) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = + \infty $.
$ \Rightarrow x = 1$ là tiệm cận đứng của đồ thị hàm số $g\left( x \right)$.
$ + \left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {2^ + }} g(x) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = – \infty } \\
{\mathop {\lim }\limits_{x \to {2^ – }} g(x) = \mathop {\lim }\limits_{x \to {2^ – }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = + \infty }
\end{array}} \right.$
$ \Rightarrow x = 2$ là tiệm cận đứng của đồ thị hàm số $g\left( x \right)$
$ + \left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {a^ + }} g(x) = \mathop {\lim }\limits_{x \to {a^ + }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = – \infty } \\
{\mathop {\lim }\limits_{x \to {a^ – }} g(x) = \mathop {\lim }\limits_{x \to {a^ – }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = + \infty }
\end{array}} \right.$
$ \Rightarrow x = a$ là tiệm cận đứng của đồ thị hàm số $g\left( x \right)$.
$ + \left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {b^ + }} g(x) = \mathop {\lim }\limits_{x \to {b^ + }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = + \infty } \\
{\mathop {\lim }\limits_{x \to {b^ – }} g(x) = \mathop {\lim }\limits_{x \to {b^ – }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = – \infty }
\end{array}} \right.$
$ \Rightarrow x = b$ là tiệm cận đứng của đồ thị hàm số $g(x)$.
$ + \left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {c^ + }} g(x) = \mathop {\lim }\limits_{x \to {c^ + }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = + \infty } \\
{\mathop {\lim }\limits_{x \to {c^ – }} g(x) = \mathop {\lim }\limits_{x \to {c^ – }} \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = – \infty }
\end{array}} \right.$
$ \Rightarrow x = c$ là tiệm cận đứng của đồ thị hàm số $g(x)$.
$ + \mathop {\lim }\limits_{x \to \pm \infty } g(x) = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{{x^2} – 3x + 2\sqrt {x – 1} }}{{x(x – 1){{(x – 2)}^2}(x – a)(x – b)(x – c)}} = 0$.
$ \Rightarrow y = 0$ là tiệm cận ngang của đồ thị hàm số $g(x)$.
Vậy đồ thị hàm số $g\left( x \right)$ có 6 đường tiệm cận.
———-
Để lại một bình luận