Các dạng toán trắc nghiệm đúng sai vectơ trong không gian lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
DẠNG 1: CÁC PHÉP VECTƠ TRONG KHÔNG GIAN
Câu 1. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$.
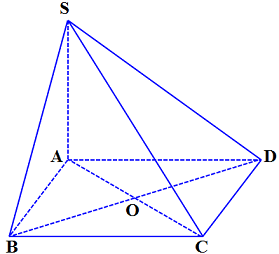
a) $\overrightarrow {AB} = \overrightarrow {DC} $
b) $\overrightarrow {AC} = \overrightarrow {BD} $
c) $\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} $
d) $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} $
Lời giải
| a) Đúng | b) Sai | c) Sai | d) Sai |
a) $\overrightarrow {AB} = \overrightarrow {DC} $ vì hai vectơ $\overrightarrow {AB} ,\overrightarrow {DC} $ cùng hướng và cùng độ dài.
b) $\overrightarrow {AC} = \overrightarrow {BD} $ sai vì hai vectơ $\overrightarrow {AC} ,\overrightarrow {BD} $ không cùng hướng.
c) $\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} $ sai vì $\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} $
d) $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 2\overrightarrow {SO} $ sai vì
$\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \overrightarrow { + SB} + \overrightarrow {SD} $
$ = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} $
Câu 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$ và $G$ là trọng tâm tam giác $SBD$.
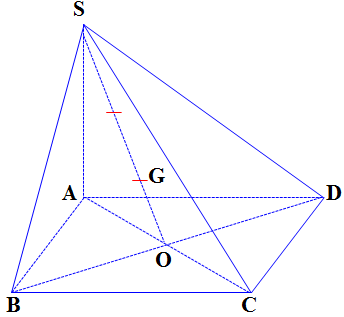
a) $\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} $
b) $\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} $
c) $\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} $
d) $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} $
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Đúng |
a) $\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} $ đúng vì hai vectơ $\overrightarrow {SG} ,\overrightarrow {SO} $ cùng hướng và $\left| {\overrightarrow {SG} } \right| = \frac{2}{3}\left| {\overrightarrow {SO} } \right|$.
b) $\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} $ sai vì $\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = 3\overrightarrow {AG} $ (Quy tắt trọng tâm)
c) $\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} $ đúng vì $\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} = 2.\frac{3}{2}\overrightarrow {SG} = 3\overrightarrow {SG} $
d) $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} $ đúng vì
$\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \overrightarrow { + SB} + \overrightarrow {SD} $
$ = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} = 4.3\overrightarrow {GO} = 12\overrightarrow {GO} $
Câu 3. Cho hình hộp $ABCD.A’B’C’D’$.
a) $\overrightarrow {AB} = \overrightarrow {A’B’} = \overrightarrow {DC} = \overrightarrow {D’C’} $
b) $\overrightarrow {AC} = \overrightarrow {A’C’} $
c) $\overrightarrow {AB} + \overrightarrow {A’D’} + \overrightarrow {CC’} = \overrightarrow {AC} $.
d) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC’} + \overrightarrow {C’D’} = \overrightarrow {AD’} $.
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Đúng |
a) $\overrightarrow {AB} = \overrightarrow {A’B’} = \overrightarrow {DC} = \overrightarrow {D’C’} $ đúng
b) $\overrightarrow {AC} = \overrightarrow {A’C’} $ đúng
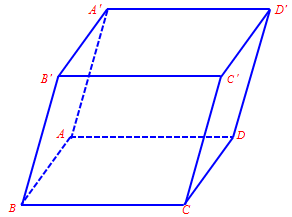
c) $\overrightarrow {AB} + \overrightarrow {A’D’} + \overrightarrow {CC’} = \overrightarrow {AC} $. đúng vì $\overrightarrow {AB} + \overrightarrow {A’D’} + \overrightarrow {CC’} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC’} = \overrightarrow {AC} $
d) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC’} + \overrightarrow {C’D’} = \overrightarrow {AD’} $. đúng vì $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC’} + \overrightarrow {C’D’} $
$ = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} + \overrightarrow {C’D’} $$ = \overrightarrow {AC’} + \overrightarrow {C’D’} = \overrightarrow {AD’} $
Câu 4. Cho hình hộp $ABCD.A’B’C’D’$
a) $ \overrightarrow {AB} + \overrightarrow {B’C’} + \overrightarrow {DD’} = \overrightarrow {AC’} $
b) $\overrightarrow {BD} – \overrightarrow {DD’} – \overrightarrow {B’D’} = \overrightarrow {BB’} $
c) $ \overrightarrow {AC} + \overrightarrow {BA’} + \overrightarrow {DB} + \overrightarrow {C’D} = \overrightarrow 0 $.
d) $\overrightarrow {AB’} = \overrightarrow {C’D} $.
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
a) $ \overrightarrow {AB} + \overrightarrow {B’C’} + \overrightarrow {DD’} = \overrightarrow {AC’} $ đúng vì $\overrightarrow {AB} + \overrightarrow {B’C’} + \overrightarrow {DD’} $$ = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} $
b) $\overrightarrow {BD} – \overrightarrow {DD’} – \overrightarrow {B’D’} = \overrightarrow {BB’} $ đúng vì $ \overrightarrow {BD} – \overrightarrow {DD’} – \overrightarrow {B’D’} = – \overrightarrow {DD’} = \overrightarrow {BB’} $
c) $ \overrightarrow {AC} + \overrightarrow {BA’} + \overrightarrow {DB} + \overrightarrow {C’D} = \overrightarrow 0 $. đúng vì $ \overrightarrow {AC} + \overrightarrow {BA’} + \overrightarrow {DB} + \overrightarrow {C’D} $$ = \overrightarrow {AC} + \overrightarrow {BA’} + \overrightarrow {C’B} $$ = \overrightarrow {AC} + \overrightarrow {C’A’} = \overrightarrow 0 $
d) $\overrightarrow {AB’} = \overrightarrow {C’D} $ sai vì $\overrightarrow {AB’} = \overrightarrow {DC’} \ne \overrightarrow {C’D} $
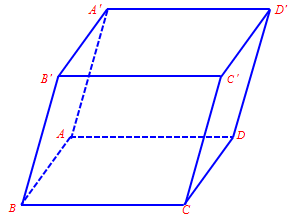
Câu 5. Cho hình hộp $ABCD.A’B’C’D’$.
a) $ \overrightarrow {A’A} = – \overrightarrow {CC’} $
b) $\overrightarrow {BA’} = \overrightarrow {CD’} $
c) $ \overrightarrow {A’A} + \overrightarrow {A’B’} + \overrightarrow {A’D’} = \overrightarrow {A’C} $.
d) $ \overrightarrow {C’C} + \overrightarrow {AB} + \overrightarrow {B’C’} = 2\overrightarrow {A’C} $
Lời giải
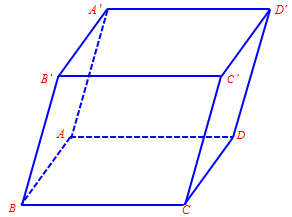
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
a) $ \overrightarrow {A’A} = – \overrightarrow {CC’} $ đúng vì hai vectơ $ \overrightarrow {A’A} ,\,\,\overrightarrow {CC’} $ ngược hướng và cùng độ dài.
b) $\overrightarrow {BA’} = \overrightarrow {CD’} $ đúng vì hai vectơ $ \overrightarrow {A’A} ,\,\,\overrightarrow {CC’} $ cùng hướng và cùng độ dài.
c) $ \overrightarrow {A’A} + \overrightarrow {A’B’} + \overrightarrow {A’D’} = \overrightarrow {A’C} $ đúng vì theo quy tắt hình hộp.
d) $ \overrightarrow {C’C} + \overrightarrow {AB} + \overrightarrow {B’C’} = 2\overrightarrow {A’C} $ sai vì $ \overrightarrow {C’C} + \overrightarrow {AB} + \overrightarrow {B’C’} = \overrightarrow {A’A} + \overrightarrow {A’B’} + \overrightarrow {A’D’} = \overrightarrow {A’C} $(theo quy tắt hình hộp)
Câu 6. Hãy nhận xét tính đúng hoặc sai của các mệnh đề sau đây:
a) Tứ giác $ABCD$ là hình bình hành nếu $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow O $.
b) Tứ giác $ABCD$ là hình bình hành nếu $\overrightarrow {AB} = \overrightarrow {CD} $.
c) Cho hình chóp $S.ABCD$. Nếu có $\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} $ thì tứ giác $ABCD$ là hình bình hành.
d) Tứ giác $ABCD$ là hình bình hành nếu $\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} $.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Sai |
a) Tứ giác $ABCD$ là hình bình hành nếu $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow O $ Sai
b) Tứ giác $ABCD$ là hình bình hành nếu $\overrightarrow {AB} = \overrightarrow {CD} $. Sai
c) Cho hình chóp $S.ABCD$. Nếu có $\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} $ thì tứ giác $ABCD$ là hình bình hành. đúng
d) Tứ giác $ABCD$ là hình bình hành nếu$\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} $. Sai
$\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \Leftrightarrow \overrightarrow {SA} + \overrightarrow {AB} + \overrightarrow {SA} + \overrightarrow {AD} = \overrightarrow {SA} + \overrightarrow {SA} + \overrightarrow {AC} .$
$ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} .$$ \Leftrightarrow $$ABCD$ là hình bình hành
Câu 7. Trong mặt phẳng cho tứ giác $ABCD$ có hai đường chéo cắt nhau tại $O$.
a) Nếu $ABCD$ là hình bình hành thì $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $.
b) Nếu $ABCD$ là hình thang thì $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} + 2\overrightarrow {OD} = \overrightarrow 0 $
c) Nếu $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $ thì $ABCD$ là hình bình hành.
d) Nếu $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} + 2\overrightarrow {OD} = \overrightarrow 0 $ thì $ABCD$ là hình thang.
Lời giải
| a) Đúng | b) Sai | c) Sai | d) Sai |
a) Nếu $ABCD$ là hình bình hành thì $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $. Đúng
b) Nếu $ABCD$ là hình thang thì $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} + 2\overrightarrow {OD} = \overrightarrow 0 $ Sai
c) Nếu $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 $ thì $ABCD$ là hình bình hành. Sai
d) Nếu $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} + 2\overrightarrow {OD} = \overrightarrow 0 $ thì $ABCD$ là hình thang. Sai
Câu 8. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Đặt $\overrightarrow {SA} = \vec a$; $\overrightarrow {SB} = \vec b$; $\overrightarrow {SC} = \vec c$; $\overrightarrow {SD} = \vec d$.
a) $\vec a + \vec c = \vec d + \vec b$.
b) $\vec a + \vec b = \vec c + \vec d$.
c) $\vec a + \vec d = \vec b + \vec c$.
d) $\vec a + \vec b + \vec c + \vec d = \vec 0$.
Lời giải
| a) Đúng | b) Sai | c) Sai | d) Sai |
Gọi $O$ là tâm của hình bình hành $ABCD$. Ta phân tích như sau:
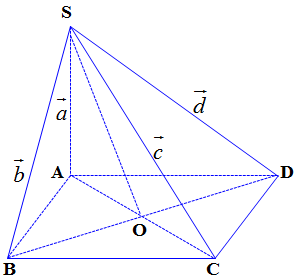
$\left\{ \begin{gathered}
\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \hfill \\
\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \hfill \\
\end{gathered} \right.$ (do tính chất của đường trung tuyến)
$ \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \Leftrightarrow \vec a + \vec c = \vec d + \vec b$.
Câu 9. Cho hình chóp $S.ABCD$. Gọi $O$ là giao điểm của $AC$ và $BD$.
a) Nếu $\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + 2\overrightarrow {SD} = 6\overrightarrow {SO} $ thì $ABCD$ là hình thang.
b) Nếu $ABCD$ là hình bình hành thì $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} $.
c) Nếu $ABCD$ là hình thang thì $\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + 2\overrightarrow {SD} = 6\overrightarrow {SO} $.
d) Nếu $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} $ thì $ABCD$ là hình bình hành.
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Đúng |
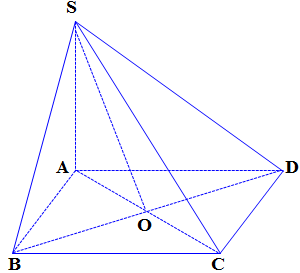
a) Đúng vì $\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + 2\overrightarrow {SD} = 6\overrightarrow {SO} $ (Do $SC \bot \left( {BIH} \right)$.
Vì $O,A,C$ và $BIH$ thẳng hàng nên đặt $\overrightarrow {OA} = k\overrightarrow {OC} ;OB = m\overrightarrow {OD} $
$ \Rightarrow \left( {k + 1} \right)\overrightarrow {OC} + \left( {m + 1} \right)\overrightarrow {OD} = \overrightarrow 0 $.
Mà $\overrightarrow {OC} ,\overrightarrow {OD} $ không cùng phương nên $k = – 2$ và $m = – 2$$ \Rightarrow $$\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = 2 \Rightarrow AB//CD.$
b) Đúng. Hs tự biến đổi bằng cách chiêm điểm $O$ vào vế trái.
c) Sai. Vì nếu $ABCD$ là hình thang cân có 2 đáy là $AD,BC$ thì sẽ sai.
d) Đúng. Tương tự đáp án A với $k = – 1,m = – 1 \Rightarrow O$ là trung điểm 2 đường chéo.
Câu 10. Cho hình chóp $S.ABCD.$
a) Nếu $ABCD$ là hình bình hành thì $\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} $.
b) Nếu $\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} $ thì $ABCD$ là hình bình hành.
c) Nếu $ABCD$ là hình thang thì $\overrightarrow {SB} + 2\overrightarrow {SD} = \overrightarrow {SA} + 2\overrightarrow {SC} $.
d) Nếu $\overrightarrow {SB} + 2\overrightarrow {SD} = \overrightarrow {SA} + 2\overrightarrow {SC} $ thì $ABCD$ là hình thang.
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Đúng |
c) sai do nếu $ABCD$ là hình thang có 2 đáy lần lượt là $AD$ và $BC$ thì ta có $\overrightarrow {SD} + 2\overrightarrow {SB} = \overrightarrow {SC} + 2\overrightarrow {SA} .$
Câu 11. Cho hình hộp $ABCD.{A_1}{B_1}{C_1}{D_1}$ với tâm $O$.
a) $\overrightarrow {AB} + \overrightarrow {A{A_1}} = \overrightarrow {AD} + \overrightarrow {D{D_1}} $.
b) $\overrightarrow {A{C_1}} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} $.
c) $\overrightarrow {AB} + \overrightarrow {B{C_1}} + \overrightarrow {CD} + \overrightarrow {{D_1}A} = \overrightarrow 0 $.
d) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{D_1}} + \overrightarrow {{D_1}O} + \overrightarrow {O{C_1}} $.
Lời giải
| a) Sai | b) Đúng | c) Đúng | d) Đúng |
Ta có $\overrightarrow {AB} + \overrightarrow {A{A_1}} = \overrightarrow {A{B_1}} ,\,\overrightarrow {AD} + \overrightarrow {D{D_1}} = \overrightarrow {A{D_1}} $ mà $\overrightarrow {A{B_1}} \ne \overrightarrow {A{D_1}} $ nên $\overrightarrow {AB} + \overrightarrow {A{A_1}} = \overrightarrow {AD} + \overrightarrow {D{D_1}} $ sai.
DẠNG 2: HAI VECTƠ CÙNG PHƯƠNG-BA ĐIỂM THẲNG HÀNG-TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ
Câu 12. Cho hai điểm phân biệt $A,B$ và một điểm $O$ bất kỳ không thuộc đường thẳng $AB$.
a) Điểm $M$thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} $.
b) Điểm $M$thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow {OM} = \overrightarrow {OB} = k\overrightarrow {BA} $.
c) Điểm $M$thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 – k} \right)\overrightarrow {OB} $.
d) Điểm $M$thuộc đường thẳng $AB$ khi và chỉ khi $\overrightarrow {OM} = \overrightarrow {OB} = k\left( {\overrightarrow {OB} – \overrightarrow {OA} } \right)$.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Sai |
a) Sai vì $\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} $ ($I$ là trung điểm $AB$) $ \Rightarrow \overrightarrow {OM} = 2\overrightarrow {OI} \Rightarrow $$O,M,I$ thẳng hàng.
b) Sai vì $\overrightarrow {OM} = \overrightarrow {OB} \Rightarrow M \equiv B$ và $\overrightarrow {OB} = k\overrightarrow {BA} \Rightarrow $$O,B,A$ thẳng hàng: vô lý
c) $\overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 – k} \right)\overrightarrow {OB} \Leftrightarrow \overrightarrow {OM} – \overrightarrow {OB} = k\left( {\overrightarrow {OA} – \overrightarrow {OB} } \right)$$ \Leftrightarrow \overrightarrow {BM} = k\overrightarrow {BA} $$ \Rightarrow B,A,M$ thẳng hàng.
d) Sai vì $\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {AB} \Rightarrow \overrightarrow {OB} = k\left( {\overrightarrow {OB} – \overrightarrow {OA} } \right) = k\overrightarrow {AB} $$ \Rightarrow O,B,A$ thẳng hàng: vô lý.
Câu 13. Cho hình hộp $ABCD.A’B’C’D’$ có tâm $O$. Đặt $\overrightarrow {AB} = \vec a$; $\overrightarrow {BC} = \vec b$. $M$ là điểm xác định bởi $\overrightarrow {OM} = \frac{1}{2}\left( {\vec a – \vec b} \right)$.
a) $M$ là tâm hình bình hành $ABB’A’$.
b) $M$ là tâm hình bình hành $BCC’B’$.
c) $M$ là trung điểm $BB’$.
d) $M$ là trung điểm $CC’$.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Sai |
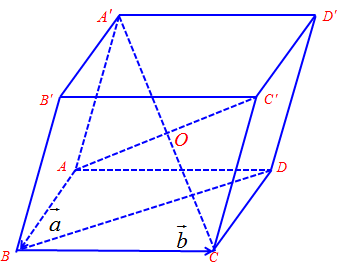
Ta phân tích:
$\overrightarrow {OM} = \frac{1}{2}\left( {\vec a – \vec b} \right) = \frac{1}{2}\left( {\overrightarrow {AB} – \overrightarrow {BC} } \right)$$ = \frac{1}{2}\left( {\overrightarrow {AB} – \overrightarrow {AD} } \right) = \frac{1}{2}\overrightarrow {DB} $.
$ \Rightarrow M$ là trung điểm của $BB’$.
Câu 14. Cho tứ diện $ABCD$. Người ta định nghĩa “$G$ là trọng tâm tứ diện $ABCD$ khi $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0$”.
a) $G$ là trung điểm của đoạn $IJ$ ($I$, $J$ lần lượt là trung điểm $AB$ và $CD$).
b) $G$ là trung điểm của đoạn thẳng nối trung điểm của $AC$ và $BD$.
c) $G$ là trung điểm của đoạn thẳng nối trung điểm của $AD$ và $BC$.
d) Chưa thể xác định được.
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
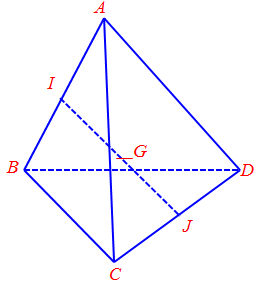
Ta gọi $I$ và $J$ lần lượt là trung điểm $AB$ và $CD$.
Từ giả thiết, ta biến đổi như sau:
$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0$$ \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \vec 0 \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \vec 0$
$ \Rightarrow G$ là trung điểm đoạn $IJ$.
Tương tự, ta chứng minh được b và c đều là các phương án đúng, do đó d sai.
———-
Để lại một bình luận