20 Câu trắc nghiệm đúng sai tính đơn điệu và cực trị của hàm số giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Câu 1: Cho hàm số $y = f(x)$ có bảng biến thiên như sau
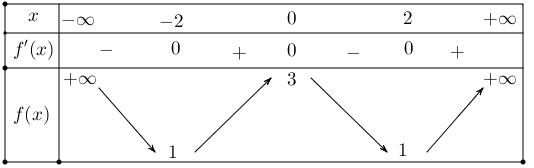
a) Hàm số nghịch biến trên khoảng $\left( { – \infty ; – 2} \right)$.
b) Hàm số đồng biến trên khoảng $\left( { – 2;0} \right)$
c) Hàm số đồng biến trên khoảng $\left( { – \infty ;0} \right)$
d) Hàm số nghịch biến trên khoảng $\left( {0;2} \right)$
Lời giải
Câu 2: Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ sau:
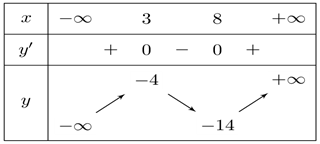
a) Hàm số $y = f\left( x \right)$ đạt cực tiểu tại $x = 3$.
b) Hàm số $y = f\left( x \right)$ đạt cực tiểu tại $x = 8$.
c) Giá trị cực đại của hàm số $y = f\left( x \right)$ bằng $ – 4$.
d) Giá trị cực đại của hàm số $y = f\left( x \right)$ bằng $ – 14$
Lời giải
Câu 3: Cho hàm số $y = f\left( x \right)$ liên tục và xác định trên $\mathbb{R}$có đồ thị đạo hàm $f’\left( x \right)$ là hàm số bậc ba như hình vẽ. Hàm số $y = f\left( x \right)$ nghịch biến trên khoảng nào sau đây?
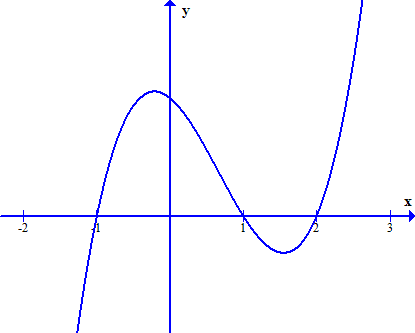
a) Hàm số nghịch biến trên khoảng $\left( { – \infty ; – 1} \right)$.
b) Hàm số đồng biến trên khoảng $\left( { – 1;1} \right)$.
c) Hàm số nghịch biến trên khoảng $\left( {0;1} \right)$.
d) Hàm số đồng biến trên khoảng $\left( {2; + \infty } \right)$.
Lời giải
Phương pháp
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.
+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
Câu 4: Cho hàm số $f\left( x \right)$ có đạo hàm là $f’\left( x \right) = \left( {x + 4} \right)\left( {x + 3} \right),\,\,\forall x \in \mathbb{R}$.
a) Hàm số nghịch biến trên khoảng $\left( { – 4; – 3} \right)$.
b) Hàm số đồng biến trên khoảng $\left( { – \infty ; – 5} \right)$.
c) Hàm số nghịch biến trên khoảng $\left( {0;1} \right)$.
d) Hàm số đồng biến trên khoảng $\left( { – 3; + \infty } \right)$.
Lời giải
Lời giải:
Ta có:
$f'(x) = 0 \Leftrightarrow \left( {x + 4} \right)\left( {x + 3} \right) = 0$
$ \Leftrightarrow \left[ \begin{gathered}
x + 4 = 0 \hfill \\
x + 3 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = – 4 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$
Bảng xét dấu $f'(x)$

Câu 5: Cho hàm số $g\left( x \right)$ có đạo hàm $g’\left( x \right) = \left( {{x^2} – 1} \right)\left( {x + 4} \right)$ với mọi $x \in \mathbb{R}$.
a) Hàm số $y = g\left( x \right)$ đạt cực đại tại $x = – 4$.
b) Hàm số $y = g\left( x \right)$ đạt cực đại tại $x = – 1$.
c) Giá trị cực tiểu của hàm số $y = g\left( x \right)$ bằng $g(1)$.
d) Giá trị cực tiểu của hàm số $y = g\left( x \right)$ bằng $g( – 1)$
Lời giải:
$g’\left( x \right) = 0 \Leftrightarrow \left( {{x^2} – 1} \right)\left( {x + 4} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
x = – 4 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
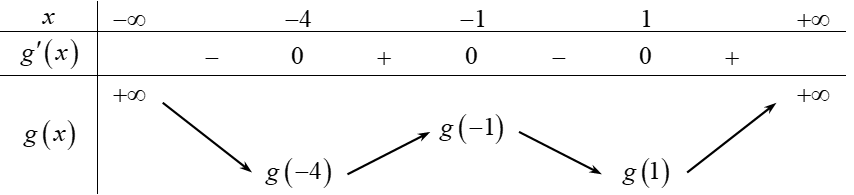
Câu 6: Cho hàm số $y = f\left( x \right)$ có bảng xét dấu đạo hàm như sau

a) Hàm số nghịch biến trên khoảng $\left( { – \infty ; – 2} \right)$.
b) Hàm số đồng biến trên khoảng $\left( { – 2;0} \right)$
c) Hàm số đồng biến trên khoảng $\left( { – \infty ;0} \right)$
d) Hàm số nghịch biến trên khoảng $\left( {0;2} \right)$
Lời giải
Theo bảng xét dấu thì $y’ < 0$ khi $x \in \left( {0;2} \right)$ nên hàm số nghịch biến trên khoảng $\left( {0;2} \right)$.
Câu 7: Cho hàm số $y = – \frac{1}{3}{x^3} + {x^2} – x + 1$.
a) Hàm số nghịch biến trên $\mathbb{R}$.
b) Hàm số đồng biến trên $\mathbb{R}$.
c) Hàm số đồng biến trên $\left( {1; + \infty } \right)$ và nghịch biến trên $\left( { – \infty ;1} \right)$.
d) Hàm số đồng biến trên $\left( { – \infty ;1} \right)$ và nghịch biến trên $\left( {1; + \infty } \right)$.
Lời giải
$y’ = – {x^2} + 2x – 1 = – {(x – 1)^2} \leqslant 0,\forall x \in \mathbb{R}$ nên hàm số nghịch biến trên $\mathbb{R}$.
Câu 8: Cho hàm số $y = \frac{{x + 3}}{{x + 2}}$.
a) Hàm số nghịch biến trên $\mathbb{R} \setminus \left\{ { – 2} \right\}$.
b) Hàm số nghịch biến trên $\left( { – \infty ; – 2} \right)$ và $\left( { – 2; + \infty } \right)$.
c) Hàm số đồng biến trên $\mathbb{R}$.
d) Hàm số đồng biến trên $\left( { – 4; – 3} \right)$.
Lời giải
$y’ = \frac{{ – 1}}{{{{(x + 2)}^2}}}$
$y’ = \frac{{ – 1}}{{{{(x + 2)}^2}}} < 0\;\forall x \in \left( { – \infty ; – 2} \right)\;$
$y’ = \frac{{ – 1}}{{{{(x + 2)}^2}}} < 0\;\forall x \in \left( { – 2; + \infty } \right)$
Câu 9: Cho hàm số $y = f\left( x \right)$. Đồ thị của hàm số $y = f’\left( x \right)$ như hình bên. Đặt $g\left( x \right) = f\left( x \right) – x$. Mệnh đề nào dưới đây đúng?
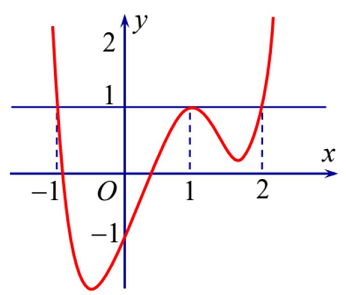
a) $g\left( 1 \right) < g\left( { – 1} \right) < g\left( 2 \right)$.
b) $g\left( { – 1} \right) < g\left( 1 \right) < g\left( 2 \right)$.
c) $g\left( 2 \right) < g\left( 1 \right) < g\left( { – 1} \right)$.
d) $g\left( 2 \right) < g\left( { – 1} \right) < g\left( 1 \right)$.
Lời giải
Xét hàm số $g\left( x \right) = f\left( x \right) – x, \Rightarrow g’\left( x \right) = f’\left( x \right) – 1$.
$g’\left( x \right) = 0 \Leftrightarrow f’\left( x \right) = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1} \\
{x = 1} \\
{x = 2}
\end{array}} \right.$
Bảng biến thiên
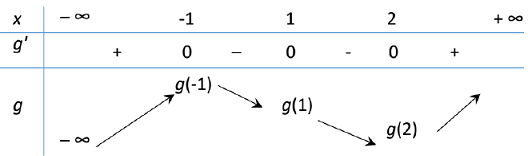
Vậy $g\left( 2 \right) < g\left( 1 \right) < g\left( { – 1} \right)$.
Câu 10: Cho hàm số $y = \frac{{{x^2} + 2x – 3}}{{x + 1}}$.
a) Hàm số đồng biến trên khoảng $\left( {2;4} \right)$.
b) Hàm số nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.
c) Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( { – 1; + \infty } \right)$.
d) Hàm số đồng biến trên khoảng $\left( { – \infty ; – 1} \right)$
Lời giải
ТХĐ: $D = R \setminus \left\{ { – 1} \right\}$.
$y’ = \frac{{{x^2} + 2x + 5}}{{{{(x + 1)}^2}}} > 0,\;\forall x \ne – 1$.
Suy ra Hàm số đồng biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( { – 1; + \infty } \right)$.
Do đó đồng biến trên khoảng $\left( {2;4} \right)$.
Câu 11: Cho hàm số $y = {x^3} – b{x^2} – cx + 2025$ với $b,c \in \mathbb{R}$.
a) Hàm số luôn có 2 điểm cực trị $\forall c \in \mathbb{R}$.
b) Hàm số luôn có 2 điểm cực trị $\forall c \in \left( { – \infty ;0} \right)$.
c) Hàm số luôn có 2 điểm cực trị $\forall c \in \left( {0; + \infty } \right)$.
d) Hàm số luôn có 2 điểm cực trị $\forall c \in \mathbb{Z}$.
Lời giải
$y = {x^3} – {x^2} – cx + 2025$ có tập xác định là: $D = \mathbb{R}$
$y’ = 3{x^2} – 2bx – c;\Delta ‘ = {b^2} + 3c$.
Hàm số có hai điểm cực trị $ \Leftrightarrow $ phương trình $y’ = 0$ có hai nghiệm phân biệt
$ \Leftrightarrow $$\Delta ‘ = {b^2} + 3c > 0$
a) Hàm số luôn có 2 điểm cực trị $\forall c \in \mathbb{R}$ Sai.
Ta chọn $b = 0,\,c = – 1 \Rightarrow \Delta ‘ = – 3 < 0$
b) Hàm số luôn có 2 điểm cực trị $\forall c \in \left( { – \infty ;0} \right)$ Sai.
Ta chọn $b = 0,\,c = – 1 \Rightarrow \Delta ‘ = – 3 < 0$
c) Hàm số luôn có 2 điểm cực trị $\forall c \in \left( {0; + \infty } \right)$ Đúng
Ta có: $\left\{ \begin{gathered}
{b^2} > 0 \hfill \\
c > 0 \hfill \\
\end{gathered} \right. \Rightarrow \Delta ‘ > 0$
d) Hàm số luôn có 2 điểm cực trị $\forall c \in \mathbb{Z}$ Sai
Ta chọn $b = 0,\,c = – 1 \Rightarrow \Delta ‘ = – 3 < 0$
Câu 12: Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau
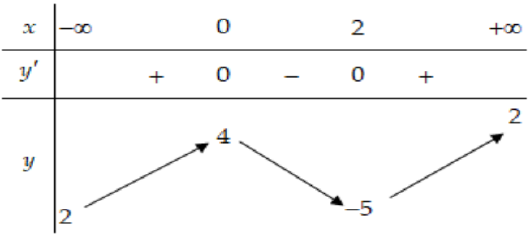
a) Hàm số đạt cực tiểu tại $x = – 5$
b) Hàm số có bốn điểm cực trị
c) Hàm số đạt cực tiểu tại $x = 2$
d) Hàm số không có cực đại
Lời giải
Dựa vào bảng biến thiên. Hàm số có đạo hàm trên $\mathbb{R}$ và $y’\left( 2 \right) = 0;y’$ đổi dấu từ âm sang dương khi đi qua $x = 2$ nên hàm số đạt cực tiểu tại $x = 2$.
Câu 13: Cho hàm số $y = \frac{{{x^2} + 3}}{{x + 1}}$.
a) Cực tiểu của hàm số bằng -3
b) Cực tiểu của hàm số bằng 1
c) Cực tiểu của hàm số bằng -6
d) Cực tiểu của hàm số bằng 2
Lời giải
Cách 1.
Ta có: $y’ = \frac{{{x^2} + 2x – 3}}{{{{(x + 1)}^2}}}$;
$y’ = 0 \Leftrightarrow {x^2} + 2x – 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 3} \\
{x = 1}
\end{array}} \right.$
Bảng biến thiên
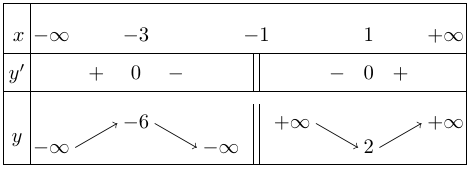
Vậy hàm số đạt cực tiểu tại $x = 1$ và giá trị cực tiểu bằng 2 .
Cách 2.
Ta có $y’ = \frac{{{x^2} + 2x – 3}}{{{{(x + 1)}^2}}};$
$y’ = 0 \Leftrightarrow {x^2} + 2x – 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 3} \\
{x = 1}
\end{array}} \right.$
$y” = \frac{8}{{{{(x + 1)}^3}}}$.
Khi đó: $y”\left( 1 \right) = \frac{1}{2} > 0;$$y”\left( { – 3} \right) = – \frac{1}{2} < 0$.
Nên hàm số đạt cực tiểu tại $x = 1$ và giá trị cực tiểu bằng 2 .
Câu 14: Cho hàm số $y = {x^4} – 2{x^2} + 1$. Xét các mệnh đề sau đây
a) Hàm số có 3 điểm cực trị.
b) Hàm số đồng biến trên các khoảng $\left( { – 1;0} \right);\left( {1; + \infty } \right)$.
c) Hàm số có 1 điểm cực trị.
d) Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right);\left( {0;1} \right)$.
Lời giải
$y’ = 4{x^3} – 4x \Rightarrow y’ = 0$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}&{ \Rightarrow y = 1} \\
{x = 1}&{ \Rightarrow y = 0} \\
{x = – 1}&{ \Rightarrow y = 0}
\end{array}} \right.$
Bảng xét dấu:

Hàm số có 3 điểm cực trị, đổng biến trên khoảng $\left( { – 1;0} \right);\left( {1; + \infty } \right)$ và nghịch biến trên khoảng $\left( { – \infty ; – 1} \right);\left( {0;1} \right)$. Vậy mệnh đề $1,2,4$ đúng.
Câu 15: Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau
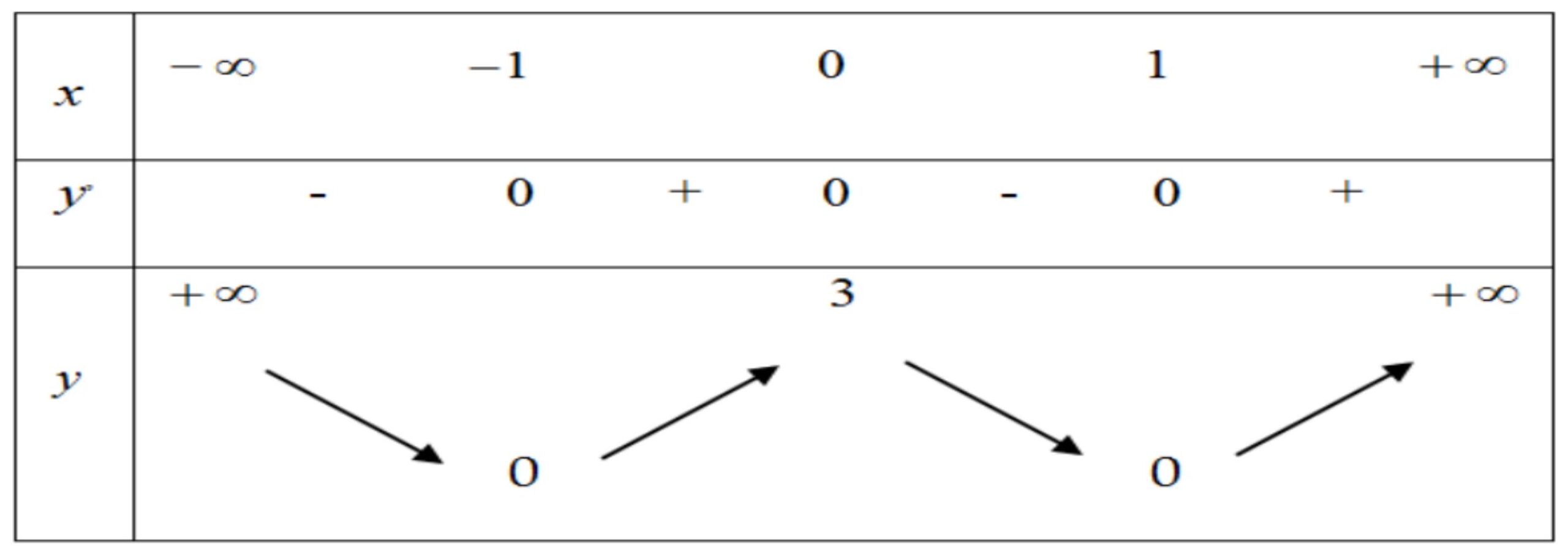
a) Hàm số có giá trị cực đại bằng 3
b) Hàm số có hai điểm cực tiểu
c) Hàm số có giá trị cực đại bằng 0
d) Hàm số có ba điểm cực trị
Lời giải
Câu 16: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = {(x + 1)^2}\left( {1 – x} \right)\left( {x + 3} \right)$. Xét tính đúng sai của các mệnh đề sau?
a) Hàm số đạt cực đại tại $x = 1$
b) Giá trị cực tiểu của hàm số là $f\left( { – 3} \right)$
c) Hàm số nghịch biến trên khoảng $\left( { – 3;1} \right)$
d) Hàm số đồng biến trên khoảng $\left( { – 3;1} \right)$
Lời giải
a) Đ
b) Đ
c) S
d) Đ
Ta có bảng biến thiên của hàm số $y = f\left( x \right)$ như sau:
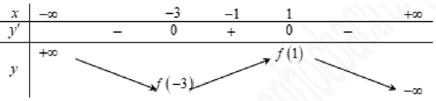
Do đó:
a) Hàm số đạt cực đại tại $x = 1$ là mệnh đề đúng
b) Giá trị cực tiểu của hàm số là $f\left( { – 3} \right)$ là mệnh đề đúng
c) Hàm số nghịch biến trên khoảng $\left( { – 3;1} \right)$ là mệnh đề sai
d) Hàm số đồng biến trên khoảng $\left( { – 3;1} \right)$ là mệnh đề đúng
Câu 17: Hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là hàm số $f’\left( x \right)$. Biết đồ thị hàm số $f’\left( x \right)$ được cho như hình vẽ.
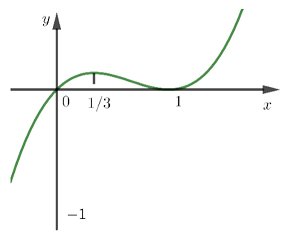
Xét tính đúng sai của các mệnh đề sau?
a) Hàm số đạt cực tiểu tại $x = 0$
b) Giá trị cực đại của hàm số là $f\left( 1 \right)$
c) Hàm số nghịch biến trên khoảng $\left( {0;1} \right)$
d) Hàm số đồng biến trên khoảng $\left( { – \infty ;1} \right)$
Lời giải
Ta có bảng biến thiên của hàm số $f\left( x \right)$ :
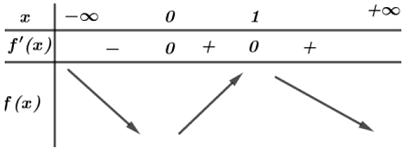
Từ bảng biến thiên ta thấy
a) Hàm số đạt cực tiểu tại $x = 0$ là mệnh đề đúng
b) Giá trị cực đại của hàm số là $f\left( 1 \right)$ là mệnh đề đúng
c) Hàm số nghịch biến trên khoảng $\left( {0;1} \right)$ là mệnh đề sai
d) Hàm số đồng biến trên khoảng $\left( { – \infty ;1} \right)$ là mệnh đề sai
Câu 18: Cho hàm số $y = \sqrt {8 + 2x – {x^2}} $. Xét tính đúng sai của các mệnh đề sau?
a) Tập xác định của hàm số là $D = \left[ { – 2;4} \right]$
b) Hàm số có $y’ = \frac{{1 – x}}{{\sqrt {8 + 2x – {x^2}} }}$
c) Hàm số nghịch biến trên khoảng $\left( {1;4} \right)$
d) Giá trị cực đại của hàm số là 0
Lời giải
Xét hàm số: $y = \sqrt {8 + 2x – {x^2}} $ có:
a) TXĐ: $D = \left[ { – 2;4} \right]$ là mệnh đề đúng
b) Ta có $y’ = \frac{{{{\left( {8 + 2x – {x^2}} \right)}’}}}{{2\sqrt {8 + 2x – {x^2}} }} = \frac{{2 – 2x}}{{2\sqrt {8 + 2x – {x^2}} }} = \frac{{1 – x}}{{\sqrt {8 + 2x – {x^2}} }}$ là mệnh đề đúng
c) Ta có $y’ = 0 \Leftrightarrow x = 1$.
Ta có bảng biến thiên:
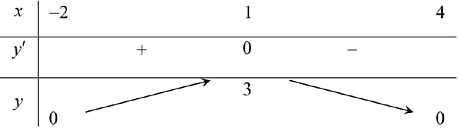
Dựa vào bảng biến thiên ta thấy
c) Hàm số nghịch biến trên khoảng $\left( {1;4} \right)$ là mệnh đề đúng
d) Giá trị cực đại của hàm số là 0 là mệnh đề sai
Câu 19: Cho hàm số $y = \frac{{2x – m}}{{x – 1}}$. Xét tính đúng sai của các mệnh đề
a) Tập xác định của hàm số là $D = \mathbb{R} \setminus \left\{ 1 \right\}$
b) Khi $m = 0$ thì đồ thị hàm số cắt trục $Ox$ tại điểm $x = 1$
c) Khi $m = – 1$ thì $y’ = \frac{{ – 3}}{{{{(x – 1)}^2}}}$
d) Hàm số đồng biến trên khoảng xác định của nó khi $m > 2$
Lời giải
a) Đ
b) Đ
c) Đ
d) $S$
a) là mệnh đề đúng
b) Khi $m = 0$ thì $y = \frac{{2x}}{{x – 1}}$.
Do đó đồ thị hàm số cắt trục $Ox$ tại điểm $x = 0$.
Do đó mệnh đề B là sai
c) Khi $m = – 1$ thì $y = \frac{{2x + 1}}{{x – 1}}$. Khi đó $y’ = \frac{{ – 3}}{{{{(x – 1)}^2}}}$ là mệnh đề đúng
d) Ta có: $y’ = \frac{{m – 2}}{{{{(x – 1)}^2}}}$.
Để hàm số đồng biến trên khoảng xác định của nó thì $y’ > 0 \Leftrightarrow \frac{{m – 2}}{{{{(x – 1)}^2}}} > 0\;\forall x \in D \Leftrightarrow m > 2$ suy ra $m \in \left( {2; + \infty } \right)$.
Do đó Mệnh đề D đúng.
Câu 20: Cho hàm số $y = \frac{{cosx – 2}}{{cosx – m}}$. Xét tính đúng sai của các mệnh đề sau?
a) Đồ thị hàm số đã cho không cắt trục $Ox$.
b) Đặt $t = cosx$ thì $0 < t < 1$
c) Khi $y = 1$ thì $m = 2$
d) Hàm số nghịch biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$ khi $m > 2$
Lời giải
a) Đồ thị hàm số đã cho không cắt trục $Ox$ là mệnh đề đúng
Vì $cosx – 2 \ne 0,\forall x \in \mathbb{R}$
b) Đặt $t = cosx$, với $x \in \left( {0;\frac{\pi }{2}} \right) \Rightarrow 0 < t < 1$ là mệnh đề đúng
c) Khi $y = 1$ thì $m = 1$
d) Hàm số nghịch biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$ khi $m > 2$
Đặt $t = cosx,0 < t < 1$ ta có hàm số: $y = \frac{{t – 2}}{{t – m}}\left( 2 \right),0 < t < 1 \Rightarrow y’ = \frac{{ – m + 2}}{{{{(t – m)}^2}}}$.
Để hàm số ban đầu nghịch biến trên khoảng $\left( {0;\frac{\pi }{2}} \right)$ thì hàm số (2) phải nghịch biến trên khoảng $(0;1)$ do đó: $\left\{ {\begin{array}{*{20}{l}}
{ – m + 2 < 0} \\
{\left[ {\begin{array}{*{20}{l}}
{m \geqslant 1} \\
{m \leqslant 0}
\end{array}} \right.}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 2} \\
{\left[ {\begin{array}{*{20}{l}}
{m \geqslant 1} \\
{m \leqslant 0}
\end{array}} \right.}
\end{array}} \right. \Leftrightarrow m > 2$.
———-
Để lại một bình luận