Các bài toán ứng dụng thực tiễn trong hệ tọa độ không gian oxyz lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Câu 1. Trong không gian với hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, một máy bay dân dụng của Mỹ đang bay với vận tốc và hướng không đổi từ điểm $A(400;150;12)$ đến điểm $B(700;250;15)$ trong $30$ phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay, hãy tính tọa độ của máy bay sau $10$ phút tiếp theo kể từ điểm $B$.
Lời giải
Gọi $C\left( {x;y;z} \right)$ là tọa độ của máy bay sau 10 phút tiếp theo.
$\overrightarrow {AB} = \left( {300;100;3} \right)$
$\overrightarrow {BC} = \left( {x – 700;y – 250;z – 15} \right)$
Do máy bay giữ nguyên hướng bay nên $\overrightarrow {AB} $ và $\overrightarrow {BC} $ cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ $A$ đến $B$ gấp $\frac{{30}}{{10}} = 3$ lần thời gian bay từ $B$ đến $C$ nên $AB = 3BC$
![]()
Suy ra $\overrightarrow {AB} = 3\overrightarrow {BC} \Leftrightarrow \left\{ \begin{gathered}
300 = 3\left( {x – 700} \right) \hfill \\
100 = 3\left( {y – 250} \right) \hfill \\
3 = 3\left( {z – 15} \right) \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered}
x = 800 \hfill \\
y = \frac{{850}}{3} \hfill \\
z = 15 \hfill \\
\end{gathered} \right. \Rightarrow Q\left( {800;\frac{{850}}{3};15} \right)$
Tọa độ của máy bay sau 5 phút tiếp theo là $\left( {800;\frac{{850}}{3};15} \right)$.
Câu 2. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm $M\left( {500;200;8} \right)$đến điểm $N\left( {800;300;10} \right)$ trong $20$ phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau $5$ phút tiếp theo bằng bao nhiêu?

Lời giải
Gọi $Q\left( {x;y;z} \right)$ là tọa độ của máy bay sau 5 phút tiếp theo.
$\overrightarrow {MN} = \left( {300;100;2} \right)$
$\overrightarrow {NQ} = \left( {x – 800;y – 300;z – 10} \right)$
Vì máy bay giữ nguyên hướng bay nên $\overrightarrow {MN} $ và $\overrightarrow {NQ} $ cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ $M$ đến $N$ gấp $\frac{{20}}{{5}} = 4$ lần thời gian bay từ $N$ đến $Q$ nên $MN = 4NQ$
Suy ra $\overrightarrow {MN} = 4\overrightarrow {NQ} \Leftrightarrow \left\{ \begin{gathered}
300 = 4\left( {x – 800} \right) \hfill \\
100 = 4\left( {y – 300} \right) \hfill \\
2 = 4\left( {z – 10} \right) \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered}
x = 875 \hfill \\
y = 325 \hfill \\
z = 10,5 \hfill \\
\end{gathered} \right. \Rightarrow Q\left( {875;325;10,5} \right)$
Tọa độ của máy bay sau 5 phút tiếp theo là $\left( {875;325;10,5} \right)$
Câu 3. Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Mỹ di chuyển với vận tốc và hướng không đổi từ điểm $M\left( {1000;600;14} \right)$ đến điểm $N$ trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo bằng $Q\left( {1400;800;16} \right)$. Xác định tọa độ vị trí điểm $N$.

Lời giải
Gọi $N\left( {x;y;z} \right)$ là tọa độ của máy bay sau 10 phút tiếp theo.
$\overrightarrow {MQ} = \left( {400;200;2} \right)$
$\overrightarrow {NQ} = \left( {1400 – x;800 – y;16 – z} \right)$
Vì máy bay giữ nguyên hướng bay nên $\overrightarrow {MQ} $ và $\overrightarrow {NQ} $ cùng hướng.
Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ $M \to Q$ gấp 4 lần thời gian bay từ $N \to Q$ nên $MQ = 4NQ$
Suy ra $\overrightarrow {MQ} = 4\overrightarrow {NQ} \Leftrightarrow \left\{ \begin{gathered}
400 = 4\left( {1400 – x} \right) \hfill \\
200 = 4\left( {800 – y} \right) \hfill \\
2 = 4\left( {16 – z} \right) \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered}
x = 1300 \hfill \\
y = 750 \hfill \\
z = 15,5 \hfill \\
\end{gathered} \right.$$ \Rightarrow N\left( {1300;750;15,5} \right)$
Tọa độ vị trí điểm $N$là $\left( {1300;750;15,5} \right)$
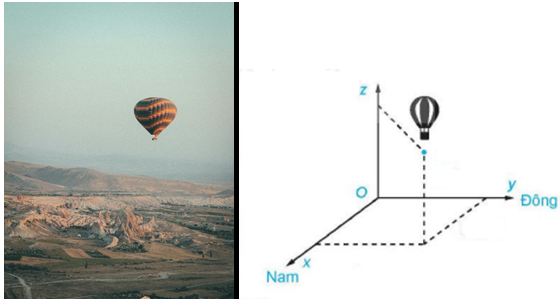
Câu 4. Một chiếc khinh khí cầu bay lên tại điểm. Sau một thời gian bay, chiếc khinh khí cầu cách điểm xuất phát về phía Đông $10\left( {km} \right)$ và về phía Nam $5\left( {km} \right)$, đồng thời cách mặt đất $400\left( m \right)$.
Chọn hệ trục tọa độ $Oxyz$, với gốc đặt tại điểm xuất phát của khinh khí cầu, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ hướng về phía Nam, trục $Oy$ hướng về phía Đông, trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
a) Tìm tọa độ của chiếc khinh khí cầu đối với hệ trục tọa độ đã chọn.
b) Xác định khoảng cách của chiếc khinh khí cầu với vị trí tại điểm xuất phát của nó.
Lời giải
a) Chiếc khinh khí cầu có tọa độ $\left( {5;10;0,4} \right)$.
b) Khoảng cách của chiếc khinh khí cầu với vị trí tại điểm xuất phát là: $\sqrt {{5^2} + {{10}^2} + {{\left( {0,4} \right)}^2}} \approx 11,2\left( {km} \right)$
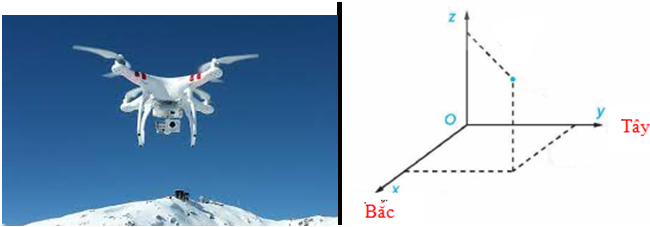
Câu 5. Một chiếc máy bay không người lái bay lên tại điểm. Sau một thời gian bay, chiếc máy bay cách điểm xuất phát về phía Bắc $50\left( {km} \right)$ và về phía Tây $20\left( {km} \right)$, đồng thời cách mặt đất $1\left( {km} \right)$.
Chọn hệ trục tọa độ $Oxyz$, với gốc đặt tại điểm xuất phát của chiếc máy bay, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ hướng về phía Bắc, trục $Oy$ hướng về phía Tây, trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
a) Tìm tọa độ của chiếc khinh khí cầu đối với hệ trục tọa độ đã chọn.
b) Xác định khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát của nó.
Lời giải
a) Chiếc máy bay có tọa độ $\left( {50;20;1} \right)$.
b) Khoảng cách của chiếc máy bay với vị trí tại điểm xuất phát là: $\sqrt {{{50}^2} + {{20}^2} + {1^2}} \approx 53,9\left( {km} \right)$
Câu 6. Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Bắc $20\left( {km} \right)$ và về phía Tây $10\left( {km} \right)$, đồng thời cách mặt đất $0,7\left( {km} \right)$. Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông $30\left( {km} \right)$ và về phía Nam $25\left( {km} \right)$, đồng thời cách mặt đất $1\left( {km} \right)$. Xác định khoảng cách giữa hai chiếc máy bay.

Lời giải
Chọn hệ trục tọa độ $Oxyz$, với gốc đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ hướng về phía Bắc, trục $Oy$ hướng về phía Tây, trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
Chiếc máy bay thứ nhất có tọa độ $\left( {20;10;0,7} \right)$.
Chiếc máy bay thứ hai có tọa độ $\left( { – 30; – 25;1} \right)$.
Do đó khoảng cách giữa hai chiếc máy bay là: $\sqrt {{{\left( {20 + 30} \right)}^2} + {{\left( {10 + 25} \right)}^2} + {{\left( {0,7 – 1} \right)}^2}} \approx 61\left( {km} \right)$
Câu 7. Hai chiếc khinh khí cầu cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc khinh khí cầu thứ nhất cách điểm xuất phát về phía Đông $100\left( {km} \right)$ và về phía Nam $80\left( {km} \right)$, đồng thời cách mặt đất $1\left( {km} \right)$. Chiếc khinh khí cầu thứ hai cách điểm xuất phát về phía Bắc $70\left( {km} \right)$ và về phía Tây $60\left( {km} \right)$, đồng thời cách mặt đất $0,8\left( {km} \right)$.

a) Xác định khoảng cách của chiếc khinh khí cầu thứ nhất với vị trí tại điểm xuất phát của nó.
b) Xác định khoảng cách giữa chiếc khinh khí cầu thứ nhất và chiếc khinh khí cầu thứ hai.
Lời giải
Chọn hệ trục tọa độ $Oxyz$, với gốc đặt tại điểm xuất phát của hai chiếc khinh khí cầu, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ hướng về phía Bắc, trục $Oy$ hướng về phía Tây, trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
Chiếc khinh khí cầu thứ nhất có tọa độ $\left( { – 100; – 80;1} \right)$.
Chiếc khinh khí cầu thứ hai có tọa độ $\left( {70;60;0,8} \right)$.
a) khoảng cách của chiếc khinh khí cầu thứ nhất với vị trí tại điểm xuất phát của nó là:
$\sqrt {{{\left( { – 100} \right)}^2} + {{\left( { – 80} \right)}^2} + {1^2}} \approx 128\left( {km} \right)$
b) khoảng cách giữa chiếc khinh khí cầu thứ nhất và chiếc khinh khí cầu thứ hai là:
$\sqrt {{{\left( { – 100 – 70} \right)}^2} + {{\left( { – 80 – 60} \right)}^2} + {{\left( {1 – 0,8} \right)}^2}} \approx 220\left( {km} \right)$
Câu 8. Ba chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Đông $60\left( {km} \right)$ và về phía Nam $40\left( {km} \right)$, đồng thời cách mặt đất $2\left( {km} \right)$. Chiếc máy bay thứ hai cách điểm xuất phát về phía Bắc $80\left( {km} \right)$ và về phía Tây $50\left( {km} \right)$, đồng thời cách mặt đất $4\left( {km} \right)$. Chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng.

a) Xác định khoảng cách giữa chiếc máy bay thứ nhất và chiếc máy bay thứ hai.
b) Xác định khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó.
Lời giải
Chọn hệ trục tọa độ $Oxyz$, với gốc đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ hướng về phía Bắc, trục $Oy$ hướng về phía Tây, trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo kilômét (xem hình vẽ).
Chiếc máy bay thứ nhất có tọa độ $\left( { – 60; – 40;2} \right)$.
Chiếc máy bay thứ hai có tọa độ $\left( {80;50;4} \right)$.
Do chiếc máy bay thứ ba nằm chính giữa của chiếc máy bay thứ nhất và thứ hai, đồng thời ba chiếc máy bay này thẳng hàng nên ở vị trí trung điểm, suy ra chiếc máy bay thứ ba có tọa độ $\left( {\frac{{ – 60 + 80}}{2};\frac{{ – 40 + 50}}{2};\frac{{2 + 4}}{2}} \right) = \left( {10;5;3} \right)$.
a) khoảng cách giữa chiếc máy bay thứ nhất và chiếc máy bay thứ hai:
$\sqrt {{{\left( { – 60 – 80} \right)}^2} + {{\left( { – 40 – 50} \right)}^2} + {{\left( {2 – 4} \right)}^2}} \approx 166,4\left( {km} \right)$
b) khoảng cách của chiếc máy bay thứ ba với vị trí tại điểm xuất phát của nó là:
$\sqrt {{{10}^2} + {5^2} + {3^2}} \approx 11,6\left( {km} \right)$
———-
Để lại một bình luận