Các dạng bài tập trả lời ngắn các phép toán vectơ trong không gian lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
DẠNG 1: CÁC PHÉP VECTƠ TRONG KHÔNG GIAN
Câu 1. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Biết $\overrightarrow {SO} = x\overrightarrow {SD} + y\overrightarrow {DA} + z\overrightarrow {SC} $. Tính $M = x + y + z$.
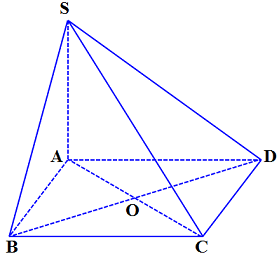
Lời giải
$\overrightarrow {SO} = \frac{1}{2}\left( {\overrightarrow {SA} + \overrightarrow {SC} } \right) = \frac{1}{2}\left( {\overrightarrow {SD} + \overrightarrow {DA} + \overrightarrow {SC} } \right)$
$ = \frac{1}{2}\overrightarrow {SD} + \frac{1}{2}\overrightarrow {DA} + \frac{1}{2}\overrightarrow {SC} $
$M = x + y + z = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} = \frac{3}{2}$.
Trả lời: $M = \frac{3}{2}$.
Câu 2. Cho hình chóp $S.ABCD$có đáy $ABCD$ là hình bình hành tâm $O$. Gọi $E$ là trung điểm của đoạn thẳng $SC$. Biểu thị $\overrightarrow {EO} $ theo ba vectơ $\overrightarrow {SB} $, $\overrightarrow {SC} $ và $\overrightarrow {SD} $ ta được $\overrightarrow {EO} = x\overrightarrow {SB} + y\overrightarrow {SC} + z\overrightarrow {SD} $ . Tính $M = x + y + z$.
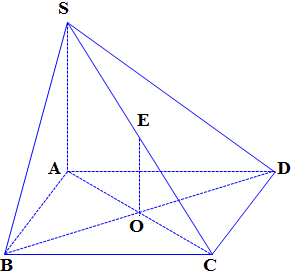
Lời giải
$\overrightarrow {EO} = \frac{1}{2}\overrightarrow {SA} = \frac{1}{2}\left( {\overrightarrow {SB} + \overrightarrow {BA} } \right) = \frac{1}{2}\left( {\overrightarrow {SB} + \overrightarrow {CD} } \right)$
$ = \frac{1}{2}\left( {\overrightarrow {SB} + \overrightarrow {SD} – \overrightarrow {SC} } \right)$$ = \frac{1}{2}\left( {\overrightarrow {SB} – \overrightarrow {SC} + \overrightarrow {SD} } \right)$
$ = \frac{1}{2}\overrightarrow {SB} – \frac{1}{2}\overrightarrow {SC} + \frac{1}{2}\overrightarrow {SD} $
$M = x + y + z = \frac{1}{2} – \frac{1}{2} + \frac{1}{2} = \frac{1}{2}$.
Trả lời: $M = \frac{1}{2}$.
Câu 3. Cho tứ diện$ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $AB$ và $CD$. Tìm giá trị của $k$ thỏa mãn đẳng thức vectơ: $\overrightarrow {MN} = k\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$
Lời giải
Trả lời: $k = \frac{1}{2}.$
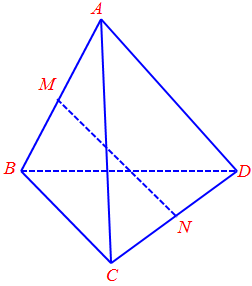
$\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right)$(quy tắc trung điểm)
$ = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {MB} + \overrightarrow {BD} } \right)$
Mà $\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 $ (vì $M$ là trung điểm $AB$)
Nên $\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.
Vậy $k = \frac{1}{2}.$
Câu 4. Cho tứ diện $ABCD$. Gọi $G$ là trọng tâm tam giác $BCD$. Biểu thị $\overrightarrow {AG} $ theo ba vectơ $\overrightarrow {AB} $, $\overrightarrow {AC} $và $\overrightarrow {AD} $ ta được $\overrightarrow {AG} = x\overrightarrow {AB} + y\overrightarrow {AC} + z\overrightarrow {AD} $ . Tính $M = x + y + z$.
Lời giải
Do $G$ là trọng tâm tam giác $BCD$ nên $\overrightarrow {AG} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)$$ = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AD} $
Vậy $M = x + y + z = \frac{1}{3} + \frac{1}{3} + \frac{1}{3} = 1$.
Câu 5. Cho tứ diện$ABCD$. Gọi $G$ là trọng tâm tam giác $BCD$. Gọi $M$ và $I$ lần lượt là trung điểm của $CD$ và $BM$. Biểu thị $\overrightarrow {AI} $ theo ba vectơ $\overrightarrow {AB} $, $\overrightarrow {AC} $ và $\overrightarrow {AD} $ ta được $\overrightarrow {AI} = x\overrightarrow {AB} + y\overrightarrow {AC} + z\overrightarrow {AD} $ . Tính $M = x + y + z$.
Lời giải
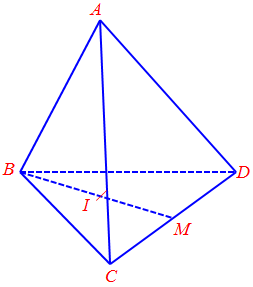
Ta có: $\overrightarrow {AG} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AM} } \right)$$ = \frac{1}{2}\left( {\overrightarrow {AB} + \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} } \right)} \right)$
$ = \frac{1}{2}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} + \frac{1}{4}\overrightarrow {AD} $
Vậy $M = x + y + z = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = 1$.
Câu 6. Cho tứ diện $ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $AB$ và $CD.$ Tìm giá trị của $k$ thỏa mãn đẳng thức vectơ: $\overrightarrow {MN} = k\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)$
Lời giải
Trả lời: $k = \frac{1}{2}$
Ta có: $\left. \begin{gathered}
\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \hfill \\
\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \hfill \\
\end{gathered} \right\}$

$ \Rightarrow 2\overrightarrow {MN} = \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {DN} + \overrightarrow {CN} $
Mà $M$ và $N$ lần lượt là trung điểm của $AB$ và $CD$ nên $\overrightarrow {MA} = \overrightarrow {BM} = – \overrightarrow {MB} ;\,\,\overrightarrow {DN} = \overrightarrow {NC} = – \overrightarrow {CN} $
Do đó $2\overrightarrow {MN} = \overrightarrow {AD} + \overrightarrow {BC} \Rightarrow \overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)$.
Vậy $k = \frac{1}{2}$
Câu 7. Gọi $M,\,N$ lần lượt là trung điểm của các cạnh $AC$ và $BD$ của tứ diện $ABCD$. Gọi $I$ là trung điểm đoạn $MN$ và $P$ là 1 điểm bất kỳ trong không gian. Tìm giá trị của $k$ thỏa mãn đẳng thức vectơ: $\overrightarrow {PI} = k\left( {\overrightarrow {PA} + \overrightarrow {PB} + \overrightarrow {PC} + \overrightarrow {PD} } \right)$.
Lời giải
Trả lời: $k = \frac{1}{4}$.
Ta có $\overrightarrow {PA} + \overrightarrow {PC} = 2\overrightarrow {PM} $, $\overrightarrow {PB} + \overrightarrow {PD} = 2\overrightarrow {PN} $
nên $\overrightarrow {PA} + \overrightarrow {PB} \overrightarrow { + PC} + \overrightarrow {PD} = 2\overrightarrow {PM} + 2\overrightarrow {PN} $
$ = 2(\overrightarrow {PM} + \overrightarrow {PN} ) = 2.2.\overrightarrow {PI} = 4\overrightarrow {PI} $.
Vậy $k = \frac{1}{4}$
Câu 8. Cho hình hộp $ABCD.A’B’C’D’$. Tìm giá trị của $k$ thỏa mãn đẳng thức vectơ: $\overrightarrow {BD} – \overrightarrow {D’D} – \overrightarrow {B’D’} = k\overrightarrow {BB’} $
Lời giải
Trả lời: $k = 1$
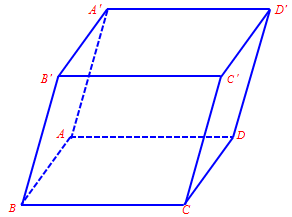
Ta có $\overrightarrow {BD} – \overrightarrow {D’D} – \overrightarrow {B’D’} =$
$\overrightarrow {BD} + \overrightarrow {DD’} + \overrightarrow {D’B’} = \overrightarrow {BB’} $ (Quy tắt hình hộp)
nên $k = 1$
Câu 9. Cho hình hộp $ABCD.{A_1}{B_1}{C_1}{D_1}$. Tìm giá trị của $k$ thỏa mãn đẳng thức vectơ: $\overrightarrow {AB} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {D{D_1}} = k\overrightarrow {A{C_1}} $
Lời giải
Trả lời: $k = 1$.
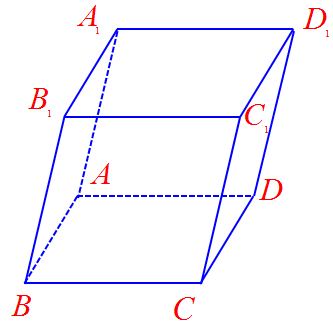
+ Ta có: $\overrightarrow {AB} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {D{D_1}} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {C{C_1}} = \overrightarrow {A{C_1}} $. (Quy tắt hình hộp)
Nên $k = 1$
DẠNG 2: PHÂN TÍCH MỘT VECTƠ THEO CÁC VECTƠ
Câu 10. Cho tứ diện $ABCD$ và $I$ là trọng tâm tam giác $ABC$. Phân tích vectơ $\overrightarrow {SI} $ theo ba vectơ $\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} $ ta được $\overrightarrow {SI} = a\overrightarrow {SA} + b\overrightarrow {SB} + c\overrightarrow {SC} $. Tính $a + b + c$.
Lời giải
Trả lời: $a + b + c = 1$.
Vì $I$ là trọng tâm tam giác $ABC$ nên $\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SI} $
$ \Leftrightarrow \overrightarrow {SI} = \frac{1}{3}\overrightarrow {SA} + \frac{1}{3}\overrightarrow {SB} + \frac{1}{3}\overrightarrow {SC} $.
Câu 11. Cho tứ diện $ABCD$ có $G$ là trọng tâm tam giác $BCD$. Đặt $\vec x = \overrightarrow {AB} $; $\vec y = \overrightarrow {AC} $; $\vec z = \overrightarrow {AD} $. Phân tích vectơ $\overrightarrow {AG} $ theo ba vectơ $\vec x,\vec y,\vec z$ ta được $\overrightarrow {AG} = a\vec x + b\vec y + c\vec z$. Tính $a + b + c$.
Lời giải
Trả lời: $a + b + c = 1$.
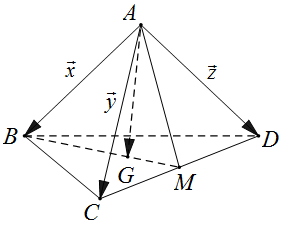
Gọi $M$ là trung điểm $CD$.
Ta phân tích:
$\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BM} $
$ = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AM} – \overrightarrow {AB} } \right)$
$ = \overrightarrow {AB} + \frac{2}{3}\left[ {\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} } \right) – \overrightarrow {AB} } \right]$
$ = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{3}\left( {\vec x + \vec y + \vec z} \right)$.
Câu 12. Cho tứ diện $ABCD$. Gọi $M$ và $P$ lần lượt là trung điểm của $AB$ và $CD$. Đặt $\overrightarrow {AB} = \overrightarrow b $, $\overrightarrow {AC} = \vec c$, $\overrightarrow {AD} = \vec d$. Phân tích vectơ $\overrightarrow {MP} $ theo ba vectơ $\vec d,\vec b,\vec c$.
Lời giải
Trả lời: $\overrightarrow {MP} = \frac{1}{2}\left( {\vec c + \vec d – \vec b} \right)$.
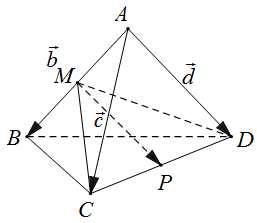
Ta phân tích:
$\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right)$ (tính chất đường trung tuyến)
$ = \frac{1}{2}\left( {\overrightarrow {AC} – \overrightarrow {AM} + \overrightarrow {AD} – \overrightarrow {AM} } \right)$
$ = \frac{1}{2}\left( {\vec c + \vec d – 2\overrightarrow {AM} } \right)$
$ = \frac{1}{2}\left( {\vec c + \vec d – \overrightarrow {AB} } \right) = \frac{1}{2}\left( {\vec c + \vec d – \vec b} \right)$.
Câu 13. Cho hình lăng trụ $ABC.A’B’C’$, $M$ là trung điểm của $BB’$. Đặt $\overrightarrow {CA} = \vec a$, $\overrightarrow {CB} = \vec b$, $\overrightarrow {AA’} = \vec c$. Phân tích vectơ $\overrightarrow {AM} $ theo ba vectơ $\vec a,\vec b,\vec c$.
Lời giải
Trả lời: $\overrightarrow {AM} = \vec b – \vec a + \frac{1}{2}\vec c$ .
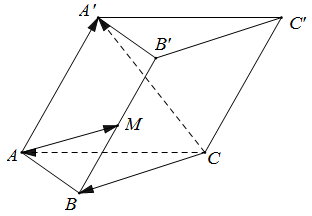
Ta phân tích như sau:
$\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {CB} – \overrightarrow {CA} + \frac{1}{2}\overrightarrow {BB’} $$ = \vec b – \vec a + \frac{1}{2}\overrightarrow {AA’} = \vec b – \vec a + \frac{1}{2}\vec c$.
DẠNG 3: HAI VECTƠ CÙNG PHƯƠNG-BA ĐIỂM THẲNG HÀNG-TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VECTƠ
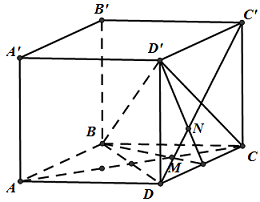
Câu 14. Cho hình hộp $ABCD.A’B’C’D’$. $M$ là điểm trên $AC$ sao cho$AC = 3MC$. Lấy $N$ trên đoạn $C’D$ sao cho $xC’D = C’N$. Với giá trị nào của $x$ thì $MN // BD’$.
Lời giải
Trả lời: $x = \frac{2}{3}$.
Câu 15. Cho hình hộp $ABCD.A’B’C’D’$. Xác định vị trí các điểm $M,N$ lần lượt trên $AC$ và $DC’$ sao cho $MN\parallel BD’$. Tính tỉ số $\frac{{MN}}{{BD’}}$.
Lời giải
Trả lời: $\frac{1}{3}$.
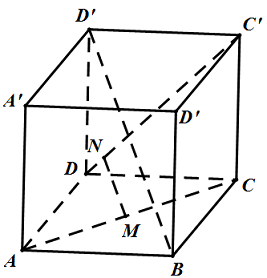
$\overrightarrow {BA} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b ,\overrightarrow {BB’} = \overrightarrow c $.
Giả sử $\overrightarrow {AM} = x\overrightarrow {AC} ,\overrightarrow {DN} = y\overrightarrow {DC’} $.
Dễ dàng có các biểu diễn $\overrightarrow {BM} = \left( {1 – x} \right)\overrightarrow a + x\overrightarrow b $ và $\overrightarrow {BN} = \left( {1 – y} \right)\overrightarrow a + \overrightarrow b + y\overrightarrow c $. Từ đó suy ra$\overrightarrow {MN} = \left( {x – y} \right)\overrightarrow a + \left( {1 – x} \right)\overrightarrow b + y\overrightarrow c \left( 1 \right)$
Để $MN\parallel BD’$ thì $\overrightarrow {MN} = z\overrightarrow {BD’} = z\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\,\left( 2 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có: $\left( {x – y} \right)\overrightarrow a + \left( {1 – x} \right)\overrightarrow b + y\overrightarrow c = z\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)$
$ \Leftrightarrow \left( {x – y – z} \right)\overrightarrow a + \left( {1 – x – z} \right)\overrightarrow b + \left( {y – z} \right)\overrightarrow c = \overrightarrow 0 \,$
$ \Leftrightarrow \left\{ \begin{gathered}
x – y – z = 0 \hfill \\
1 – x – z = 0 \hfill \\
y – z = 0 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
x = \frac{2}{3} \hfill \\
y = \frac{1}{3} \hfill \\
z = \frac{1}{3} \hfill \\
\end{gathered} \right.$.
Vậy các điểm $M,N$ được xác định bởi $\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AC} $, $\overrightarrow {DN} = \frac{1}{3}\overrightarrow {DC’} $.
Ta cũng có $\overrightarrow {MN} = z\overrightarrow {BD’} = \frac{1}{3}\overrightarrow {BD’} \Rightarrow \frac{{MN}}{{BD’}} = \frac{1}{3}$.
Câu 16. Cho hình hộp $ABCD.A’B’C’D’$. Một đường thẳng $\Delta $ cắt các đường thẳng $AA’,BC,C’D’$ lần lượt tại $M,N,P$ sao cho $\overrightarrow {NM} = 2\overrightarrow {NP} $. Tính $\frac{{MA}}{{MA’}}$.
Lời giải
Trả lời: $\frac{{MA}}{{MA’}} = 2$.
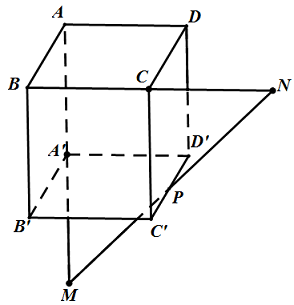
Đặt $\overrightarrow {AD} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c $.
Vì $M \in AA’$ nên $\overrightarrow {AM} = k\overrightarrow {AA’} = k\overrightarrow c $
$N \in BC \Rightarrow \overrightarrow {BN} = l\overrightarrow {BC} = l\overrightarrow a $, $P \in C’D’ \Rightarrow \overrightarrow {C’P} = m\overrightarrow b $
Ta có $\overrightarrow {NM} = \overrightarrow {NB} + \overrightarrow {BA} + \overrightarrow {AM} = – l\overrightarrow a – \overrightarrow b + k\overrightarrow c $
$\overrightarrow {NP} = \overrightarrow {BN} + \overrightarrow {BB’} + \overrightarrow {B’C’} + \overrightarrow {C’P} = (1 – l)\overrightarrow a + m\overrightarrow b + \overrightarrow c $
Do $\overrightarrow {NM} = 2\overrightarrow {NP} \Rightarrow – l\overrightarrow a – \overrightarrow b + k\overrightarrow c = 2[\left( {1 – l} \right)\overrightarrow a + m\overrightarrow b + \overrightarrow c ]$
$ \Leftrightarrow \left\{ \begin{gathered}
– l = 2\left( {1 – l} \right) \hfill \\
– 1 = 2m \hfill \\
k = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow k = 2,m = – \frac{1}{2},l = 2$.
Vậy $\frac{{MA}}{{MA’}} = 2$.
Câu 17. Cho hình hộp $ABCD.A’B’C’D’$ và các điểm $M,N,P$ xác định bởi $\overrightarrow {MA} = k\overrightarrow {MB’} \left( {k \ne 0} \right),\overrightarrow {NB} = x\overrightarrow {NC’} ,\overrightarrow {PC} = y\overrightarrow {PD’} $. Hãy tính $x,y$ theo $k$ để ba điểm $M,N,P$ thẳng hàng.
Lời giải
Trả lời: $x = \frac{{1 + k}}{{1 – k}},y = – \frac{1}{k}$ .
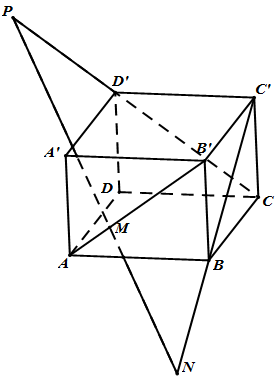
Đặt $\overrightarrow {AD} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c $.
Từ giả thiết ta có :
$\overrightarrow {AM} = \frac{k}{{k – 1}}\left( {\overrightarrow b + \overrightarrow c } \right)\left( 1 \right)$
$\overrightarrow {AN} = \overrightarrow b + \frac{x}{{x – 1}}\left( {\overrightarrow a + \overrightarrow c } \right)\left( 2 \right)$
$\overrightarrow {AP} = \overrightarrow a + \overrightarrow b + \frac{y}{{y – 1}}\left( {\overrightarrow c – \overrightarrow b } \right)\left( 3 \right)$
Từ đó ta có
$\overrightarrow {MN} = \overrightarrow {AN} – \overrightarrow {AM} $$ = \frac{x}{{x – 1}}\overrightarrow a – \frac{1}{{k – 1}}\overrightarrow b + \left( {\frac{x}{{x – 1}} – \frac{k}{{k – 1}}} \right)\overrightarrow c $
$ + \left( {\frac{x}{{x – 1}} – \frac{y}{{y – 1}}} \right)\overrightarrow c $.
$\overrightarrow {MP} = \overrightarrow {AP} – \overrightarrow {AM} $$ = \overrightarrow a – (\frac{y}{{y – 1}} + \frac{1}{{k – 1}})\overrightarrow b + \left( {\frac{y}{{y – 1}} – \frac{k}{{k – 1}}} \right)\overrightarrow c $
Ba điểm $M,N,P$ thẳng hàng khi và chỉ khi tồn tại $\lambda $ sao cho $\overrightarrow {MN} = \lambda \overrightarrow {MP} \left( * \right)$.
Thay các vec tơ $\overrightarrow {MN} ,\overrightarrow {MP} $ vào $\left( * \right)$ và lưu ý $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ không đồng phẳng ta tính được $x = \frac{{1 + k}}{{1 – k}},y = – \frac{1}{k}$.
Câu 18. Cho tứ diện $ABCD$. Gọi $I,J$ lần lượt là trung điểm của $AB$ và $CD$, $G$ là trung điểm của $IJ$.
a) Giả sử $a.\overrightarrow {IJ} = \overrightarrow {AC} + \overrightarrow {BD} $ thì giá trị của $a$ bằng bao nhiêu?
b) Xác định vị trí của $M$ để $\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|$ nhỏ nhất.
Lời giải
Trả lời:
a) $a = 2$
b) vị trí của $M$ trùng với G
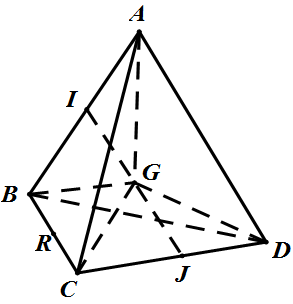
a) $\left\{ \begin{gathered}
\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AC} + \overrightarrow {CJ} \hfill \\
\overrightarrow {IJ} = \overrightarrow {IB} + \overrightarrow {BD} + \overrightarrow {DJ} \hfill \\
\end{gathered} \right. \Rightarrow $$2\overrightarrow {IJ} = \overrightarrow {AC} + \overrightarrow {BD} $.
b) Ta có$\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right| = 4\left| {\overrightarrow {MG} } \right|$ nên $\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right|$ nhỏ nhất khi $M \equiv G$.
Câu 19. Trong không gian cho tam giác $ABC$. Tìm $M$ sao cho giá trị của biểu thức $P = M{A^2} + M{B^2} + M{C^2}$ đạt giá trị nhỏ nhất.
Lời giải
Trả lời: $M$ là trọng tâm tam giác $ABC$.
Gọi$G$ là trọng tâm tam giác $ABC \Rightarrow G$ cố định và $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 .$
$P = {\left( {\overrightarrow {MG} + \overrightarrow {GA} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GB} } \right)^2} + {\left( {\overrightarrow {MG} + \overrightarrow {GC} } \right)^2}$
$ = 3M{G^2} + 2\overrightarrow {MG} .\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)$$ + G{A^2} + G{B^2} + G{C^2}$
$ = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}$$ \geqslant G{A^2} + G{B^2} + G{C^2}.$
Dấu bằng xảy ra $ \Leftrightarrow M \equiv G.$
Vậy ${P_{\min }} = G{A^2} + G{B^2} + G{C^2}$ với $M \equiv G$ là trọng tâm tam giác $ABC.$
DẠNG 4: BÀI TOÁN THỰC TIỄN ỨNG DỤNG VECTƠ TRONG KHÔNG GIAN
Câu 20. Một tấm sắt tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không giãn xuất phát từ điểm $O$ trên trần nhà và lần lượt buộc vào ba điểm $A,B,C$ trên tấm sắt tròn sao cho các lực căng $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} $ lần lượt trên mỗi dây $OA,OB,OC$ đôi một vuông góc với nhau và có độ lớn bằng nhau $\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|$ . Biết trọng lượng $P$ của tấm sắt tròn đó bằng $2024\sqrt 3 \left( N \right)$ (xem hình vẽ).
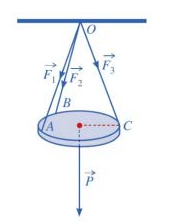
Tính lực căng của dây treo tấm sắt tròn đó.
Lời giải
Trả lời: $\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = 2024\left( N \right)$
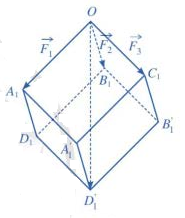
Gọi ${A_1},{B_1},{C_1}$ lần lượt là các điểm sao cho $\overrightarrow {O{A_1}} = \overrightarrow {{F_1}} ,\,\overrightarrow {O{B_1}} = \overrightarrow {{F_2}} ,\,\overrightarrow {O{C_1}} = \overrightarrow {{F_3}} $
Lấy các điểm ${D_1},A_1’,B_1’,D_1’$ sao cho $O{A_1}{D_1}{B_1}.{C_1}A_1’D_1’B_1’$ là hình hộp .
Theo quy tắc hình hộp ta có: $\overrightarrow {O{A_1}} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} = \overrightarrow {OD_1’} $
Do các lực căng $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} $ đôi một vuông góc với nhau và có độ lớn: $\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|$ nên hình hộp $O{A_1}{D_1}{B_1}.{C_1}A_1’D_1’B_1’$ có ba cạnh $OA,OB,OC$ đôi một vuông góc và bằng nhau. Vì thế $O{A_1}{D_1}{B_1}.{C_1}A_1’D_1’B_1’$ là hình lập phương có độ dài cạnh bằng $\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = x$, suy ra độ dài đường chéo bằng $\sqrt 3 x$
Vì tấm gỗ tròn ở vị trí cân bằng nên: $\overrightarrow P = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} $
Ta có: $\left| {\overrightarrow P } \right| = \left| {\overrightarrow {OD_1’} } \right| \Leftrightarrow 2024\sqrt 3 = \sqrt 3 x \Leftrightarrow x = 2024\left( N \right)$
———-
Để lại một bình luận