Cách tìm tiệm cận đứng ngang dựa vào bảng biến thiên được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.
I. Tìm tiệm cận đứng của đồ thị hàm số dựa vào bảng biến thiên
1. Phương pháp
Bước 1: Tìm các giá trị ${x_0}$ mà hàm số không xác định (Dấu hai gạch dọc).
Bước 2: Sử dụng định nghĩa đường tiệm cận đứng.
Đường thẳng $x = {x_0}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau đây thỏa mãn:
$\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = – \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = – \infty $.
2. Các ví dụ
Ví dụ 1. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.
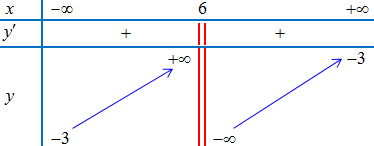
Lời giải
Hàm số không xác định tại ${x_0} = 6$.
Ta có:
$\mathop {\lim }\limits_{x \to {6^ + }} y = – \infty $; $\mathop {\lim }\limits_{x \to {6^ + }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 6$
Ví dụ 2. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.
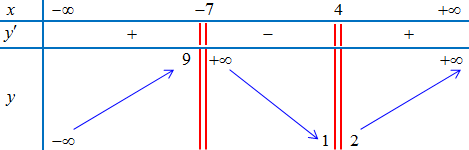
Lời giải
Hàm số không xác định tại ${x_0} = – 7$ và ${x_0} = 4$.
* Ta có:
$\mathop {\lim }\limits_{x \to – {7^ + }} y = + \infty $; $\mathop {\lim }\limits_{x \to – {7^ – }} y = 9$
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = – 7$.
* Ta có:
$\mathop {\lim }\limits_{x \to {4^ + }} y = 2$; $\mathop {\lim }\limits_{x \to {4^ – }} y = 1$
$ \Rightarrow $ Đường thẳng $x = 4$ không phải là tiệm cận đứng của đồ thị hàm số.
Vậy, hàm số có tiệm đứng là $x = – 7$.
Ví dụ 3. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận đứng của đồ thị hàm số $y = f(x)$.
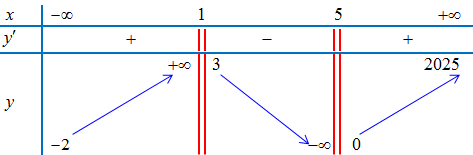
Lời giải
Hàm số không xác định tại ${x_0} = 1$ và ${x_0} = 5$.
* Ta có:
$\mathop {\lim }\limits_{x \to {1^ + }} y = 3$; $\mathop {\lim }\limits_{x \to {1^ – }} y = + \infty $
$ \Rightarrow $ Đường thẳng $x = 1$ là tiệm cận đứng của đồ thị hàm số.
* Ta có:
$\mathop {\lim }\limits_{x \to {5^ + }} y = 0$; $\mathop {\lim }\limits_{x \to {5^ + }} y = – \infty $
$ \Rightarrow $ Đường thẳng $x = 5$ là tiệm cận đứng của đồ thị hàm số.
Vậy, hàm số có hai tiệm đứng là $x = 1$; $x = 5$.
II. Tìm tiệm cận ngang của đồ thị hàm số
1. Phương pháp:
Sử dụng định nghĩa: Đường thẳng $y = {y_0}$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu $\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to – \infty } f(x) = {y_0}$.
2. Các ví dụ
Ví dụ 4. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.
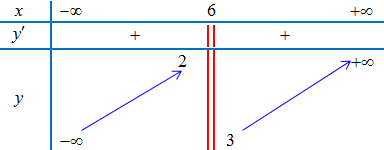
Lời giải
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = + \infty $; $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $
$ \Rightarrow $ Đồ thị hàm số không có tiệm cận ngang.
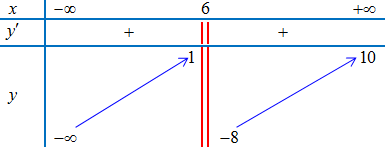
Ví dụ 5. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.
Lời giải
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = 10$; $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 10$.
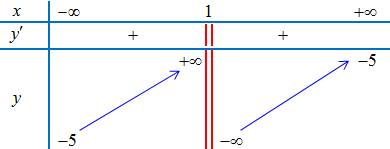
Ví dụ 6. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.
Lời giải
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = – 5$; $\mathop {\lim }\limits_{x \to – \infty } y = – 5$
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = – 5$.
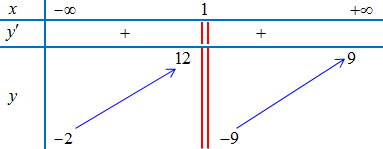
Ví dụ 7. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.
Lời giải
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = 9$; $\mathop {\lim }\limits_{x \to – \infty } y = – 2$
$ \Rightarrow $ Đồ thị hàm số có hai tiệm cận ngang là đường thẳng $y = 9$ và $y = – 2$.
Chú ý: Đồ thị hàm số $y = f(x)$ có tối đa hai tiệm cận ngang.
Ví dụ 8. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ dưới. Tìm tiệm cận ngang của đồ thị hàm số $y = f(x)$.

Lời giải
* Tìm tiệm cận đứng
Hàm số không xác định tại ${x_0} = – 1$và ${x_0} = 7$.
Ta có:
$\mathop {\lim }\limits_{x \to – {1^ + }} y = 2$; $\mathop {\lim }\limits_{x \to – {1^ – }} y = 3$
$ \Rightarrow $ Đường thẳng $x = – 1$ không phải là tiệm cận đứng của đồ thị hàm số.
$\mathop {\lim }\limits_{x \to {7^ + }} y = – \infty $; $\mathop {\lim }\limits_{x \to {7^ + }} y = – 6$
$ \Rightarrow $ Đường thẳng $x = 7$ là tiệm cận đứng của đồ thị hàm số.
* Tìm tiệm cận ngang
Ta có:
$\mathop {\lim }\limits_{x \to + \infty } y = 20$; $\mathop {\lim }\limits_{x \to – \infty } y = – \infty $
$ \Rightarrow $ Đồ thị hàm số có tiệm cận ngang là đường thẳng $y = 20$.
Vậy, đồ thị hàm số có tiệm cận đứng là đường thẳng $x = 7$ và tiệm cận ngang là đường thẳng $y = 20$.
———-
Để lại một bình luận