Phương pháp:
* Đường thẳng $x = {x_0}$ được gọi là đường tiệm cận đứng của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau đây thỏa mãn:
$\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = – \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = + \infty $; $\mathop {\lim }\limits_{x \to {x_0}^ – } f(x) = – \infty $.
* Đường thẳng $y = {y_0}$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu $\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to – \infty } f(x) = {y_0}$.
* Đường thẳng $y = ax + b$ $(a \ne 0)$ gọi là đường tiệm cận xiên của đồ thị hàm số $y = f(x)$ nếu $\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) – (ax + b)} \right] = 0$ hoặc $\mathop {\lim }\limits_{x \to – \infty } \left[ {f(x) – (ax + b)} \right] = 0$
Câu 1. Tiệm cận đứng của đồ thị hàm số $y = \frac{{x + 2}}{{x + 1}}$ là:
A. $x = – 1$.
B. $x = – 2$.
C. $x = 1$.
D. $x = 2$.
Lời giải
Chọn A
$\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty ;\,\mathop {\lim }\limits_{x \to – {1^ – }} y = – \infty $
$ \Rightarrow x = – 1$ là tiệm cận đứng của đồ thị hàm số
Câu 2. Tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 3x + 5}}{{x + 2}}$ là:
A. $y = x$.
B. $y = x + 1$.
C. $y = x + 2$.
D. $y = x + 3$.
Lời giải
Chọn B
Ta có: $y = \frac{{{x^2} + 3x + 5}}{{x + 2}} = x + 1 + \frac{3}{{x + 2}}$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là: $y = x + 1$
Câu 3. Đồ thị hàm số ở Hình $18a$, Hình $18b$ đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?
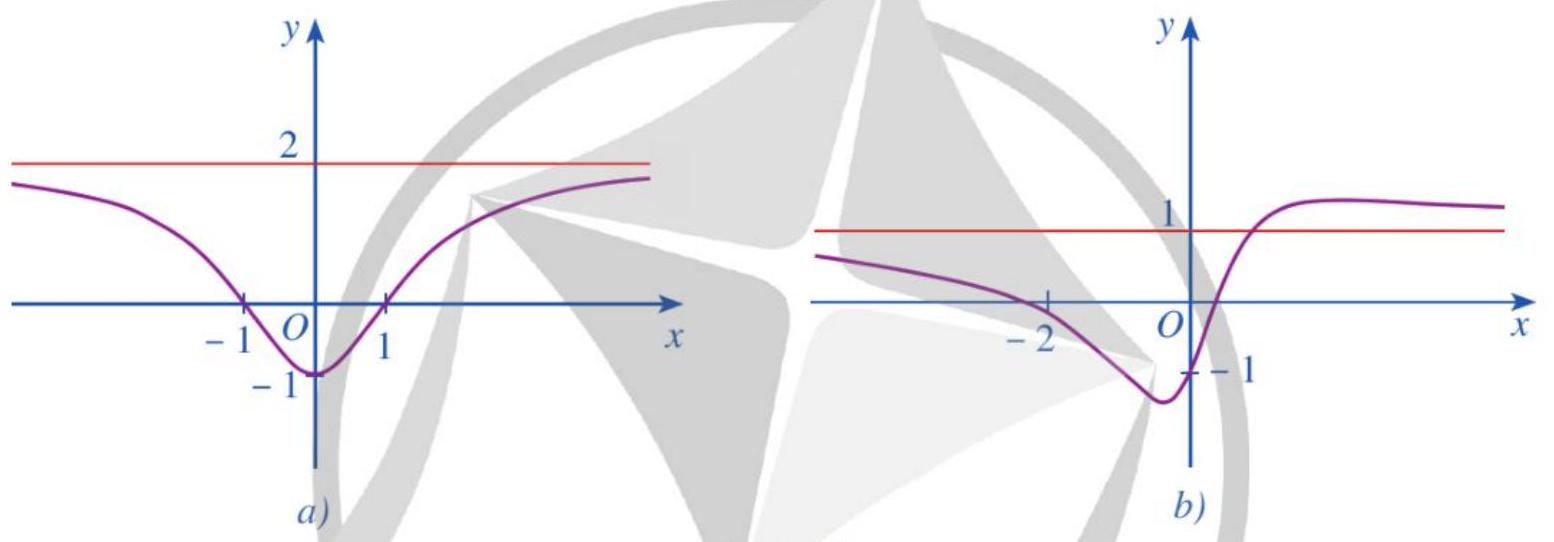
Hình 18
a) $y = \frac{{{x^2} + 2x – 1}}{{{x^2} + 1}}$;
b) $y = \frac{{2{x^2} + x + 1}}{{x – 1}}$;
c) $y = \frac{{2{x^2} – 2}}{{{x^2} + 2}}$.
Lời giải
* ở Hình $18a$ có tiệm cận ngang là đường thẳng $y = 2$ của đồ thị hàm số a.
* ở Hình $18b$ có tiệm cận ngang là đường thẳng $y = 1$ của đồ thị hàm số b, c.
Câu 4. Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:
a) $y = \frac{x}{{2 – x}}$;
b) $y = \frac{{2{x^2} – 3x + 2}}{{x – 1}}$;
c) $y = x – 3 + \frac{1}{{{x^2}}}$
Lời giải
a) $y = \frac{x}{{2 – x}}$;
* $\mathop {\lim }\limits_{x \to {2^ + }} y = – \infty ;\,\mathop {\lim }\limits_{x \to {2^ – }} y = + \infty $
$ \Rightarrow x = 2$ là tiệm cận đứng của đồ thị hàm số.
* $\mathop {\lim }\limits_{x \to + \infty } y = – 1;\,\mathop {\lim }\limits_{x \to – \infty } y = – 1$
$ \Rightarrow y = – 1$ là tiệm cận ngang của đồ thị hàm số.
b) * Ta có: $y = \frac{{2{x^2} – 3x + 2}}{{x – 1}} = 2x – 1 + \frac{1}{{x – 1}}$;
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là: $y = 2x – 1$.
* $\mathop {\lim }\limits_{x \to {2^ + }} y = – \infty ;\,\mathop {\lim }\limits_{x \to {2^ – }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 2$.
c) * Ta có: $y = x – 3 + \frac{1}{{{x^2}}}$
$ \Rightarrow $ Tiệm cận xiên của đồ thị hàm số là: $y = x – 3$.
* $\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ;\,\mathop {\lim }\limits_{x \to {0^ – }} y = + \infty $
$ \Rightarrow $ Tiệm cận đứng của đồ thị hàm số là $x = 0$.
Câu 5. Số lượng sản phẩm bán được của một công ty trong $x$ (tháng) được tính theo công thức $S\left( x \right) = 200\left( {5 – \frac{9}{{2 + x}}} \right)$, trong đó $x \geqslant 1$ (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
a) Xem $y = S\left( x \right)$ là một hàm số xác định trên nửa khoảng $\left[ {1; + \infty } \right)$, hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong $x$ (tháng) khi $x$ đủ lớn.
Lời giải
a) Ta có: $S\left( x \right) = 200\left( {5 – \frac{9}{{2 + x}}} \right) = 1000 – \frac{{1800}}{{2 + x}}$
* $\mathop {\lim }\limits_{x \to + \infty } y = 1000$
$ \Rightarrow y = 1000$ là tiệm cận ngang của đồ thị hàm số.
b) Khi $x$ đủ lớn ta có: $\mathop {\lim }\limits_{x \to + \infty } y = 1000$, tức là số lượng sản phẩm bán tối đa là $1000$ (sản phẩm)
———-
Để lại một bình luận