Trắc nghiệm đúng sai ứng dụng đạo hàm để giải quyết vấn đề thực tiễn giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.
Câu 1. Số dân của một thị trấn sau $t$ năm kề từ năm 1970 được ước tính bởi công thức $f(t) = \frac{{26t + 10}}{{t + 5}}$ ( $(f(t)$ được tính bằng nghìn người).
a) Số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
b) Số dân của thị trấn vào đầu năm 1995 là 23 nghìn người.
c) Xem $f$ là một hàm số xác định trên nửa khoảng $\left[ {0; + \infty } \right)$. Vậy hàm số đồng biến trên $\left[ {0; + \infty } \right)$.
d) Đạo hàm của hàm số $f$ biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn nguời/năm). Vào năm 1998 thì tốc độ tăng dân số là 0,125 nghìn người/năm
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
a) Vào đầu năm 1980 , ta có $t = 1980 – 1970 = 10$$ \Rightarrow f\left( {10} \right) = 18$.
Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
b) Vào đầu năm 1995, ta có $t = 25;f\left( {25} \right) = 22$.
Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.
c) $f’\left( t \right) = \frac{{120}}{{{{(t + 5)}^2}}}$ với mọi $t > 0;f\left( t \right)$ liên tục trên $\left[ {0; + \infty } \right)$ (vì liên tục trên khoảng $\left( { – 5; + \infty } \right)$ )
Vậy hàm số đồng biến trên $\left[ {0; + \infty } \right)$.
d) Tốc độ tăng dân số vào đầu năm 1998 là
$f'(28) = \frac{{120}}{{{{\left( {28 + 5} \right)}^2}}} = \frac{{40}}{{363}} \approx 0,11$ (Chú ý $t = 1998 – 1970 = 28$)
Bài tập tương tự:
Số dân của một thành phố sau $t$ năm kể từ năm 2000 được ước tính bởi công thức $g(t) = \frac{{30t + 20}}{{t + 10}}$ (trong đó $g(t)$ được tính bằng nghìn người).
a) Số dân của thành phố vào đầu năm 2010 là 40 nghìn người.
b) Số dân của thành phố vào đầu năm 2020 là 50 nghìn người.
c) Xem $g$ là một hàm số xác định trên nửa khoảng $\left[ {0; + \infty } \right)$. Vậy hàm số đồng biến trên $\left[ {0; + \infty } \right)$.
d) Đạo hàm của hàm số $g$ biểu thị tốc độ tăng dân số của thành phố (tính bằng nghìn người/năm). Vào năm 2025 thì tốc độ tăng dân số là 0,048 nghìn người/năm.
Lời giải
| a) Sai | b) Sai | c) Đúng | d) Sai |
Số dân của một thành phố sau $t$ năm kể từ năm 2000 được ước tính bởi công thức $g(t) = \frac{{30t + 20}}{{t + 10}}$ (trong đó $g(t)$ được tính bằng nghìn người).
a) Số dân của thành phố vào đầu năm 2010 là 40 nghìn người.
Để tính số dân vào đầu năm 2010, ta cần tính $g(t)$ tại $t = 2010 – 2000 = 10$.
$g(10) = \frac{{30 \cdot 10 + 20}}{{10 + 10}} = \frac{{300 + 20}}{{20}} = \frac{{320}}{{20}} = 16$
Ý a) sai, vì số dân là 16 nghìn người, không phải 40 nghìn người.
b) Số dân của thành phố vào đầu năm 2020 là 50 nghìn người.
Để tính số dân vào đầu năm 2020, ta cần tính $g(t)$ tại $t = 2020 – 2000 = 20$.
$g(20) = \frac{{30 \cdot 20 + 20}}{{20 + 10}} = \frac{{600 + 20}}{{30}} = \frac{{620}}{{30}} = 20.67$
Ý b) sai, vì số dân là khoảng 20.67 nghìn người, không phải 50 nghìn người.
c) Xem $g$ là một hàm số xác định trên nửa khoảng $\left[ {0; + \infty } \right)$. Vậy hàm số đồng biến trên $\left[ {0; + \infty } \right)$.
Để kiểm tra tính đồng biến của hàm số $g$ trên $\left[ {0; + \infty } \right)$, ta cần tính đạo hàm $g'(t)$ và kiểm tra dấu của nó.
$g(t) = \frac{{30t + 20}}{{t + 10}}$
$g'(t) = \frac{{280}}{{{{(t + 10)}^2}}}$
Vì ${(t + 10)^2} > 0$ với mọi $t \geqslant 0$, nên $g'(t) > 0$ với mọi $t \geqslant 0$. Điều này có nghĩa là $g(t)$ đồng biến trên $\left[ {0; + \infty } \right)$.
Ý c) đúng.
d) Đạo hàm của hàm số $g$ biểu thị tốc độ tăng dân số của thành phố (tính bằng nghìn người/năm). Vào năm 2025 thì tốc độ tăng dân số là 0,048 nghìn người/năm.
Để tính tốc độ tăng dân số vào năm 2025, ta cần tính $g'(t)$ tại $t = 2025 – 2000 = 25$.
$g'(25) = \frac{{280}}{{{{(25 + 10)}^2}}} = \frac{{280}}{{{{35}^2}}} = \frac{{280}}{{1225}} \approx 0.2286$
Ý d) sai, vì tốc độ tăng dân số là khoảng 0.2286 nghìn người/năm, không phải 0.048 nghìn người/năm.
Câu 2. Dân số của một quốc gia sau $t$ (năm) kể từ năm 2023 được ước tính bởi công thức:
$N\left( t \right) = 100{e^{0,012t}}(N\left( t \right)$ được tính bằng triệu người, $0 \leqslant t \leqslant 50)$
a) Dân số của quốc gia vào năm 2030 là: 108, 763 (triệu người)
b) Dân số của quốc gia vào năm 2035 là: 125,488 (triệu người)
c) Xem $N\left( t \right)$ là hàm số của biến số $t$ xác định trên đoạn $\left[ {0;50} \right]$. Khi đó hàm số $N\left( t \right)$ đồng biến trên đoạn $\left[ {0;50} \right]$.
d) Đạo hàm của hàm số $N\left( t \right)$ biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vậy vào năm 2040 thì tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm.
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
a) Dân số của quốc gia vào năm 2030 là: $N\left( 7 \right) = 100{e^{0,012.7}} = 100{e^{0,084}} = 108,763$ (triệu người)
b) Dân số của quốc gia vào năm 2035 là: $N\left( {12} \right) = 100{e^{0,012.12}} = 100{e^{0,144}} = 115,488$ (triệu người)
c) Trên đoạn $\left[ {0;50} \right]$ ta có: $N’\left( t \right) = 0,012.100{e^{0,012t}} = 1,2{e^{0,012t}} > 0,\forall t \in \left[ {0;50} \right]$
Do đó, hàm số $N\left( t \right)$ đồng biến trên đoạn $\left[ {0;50} \right]$.
d) Ta có: $N’\left( t \right) = 1,2{e^{0,012t}}$
Với tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm ta có:
$1,6 = 1,2{e^{0,012t}} \Leftrightarrow {e^{0,012t}} = \frac{4}{3}$ $ \Leftrightarrow t = \frac{{250ln\frac{4}{3}}}{3} \approx 23,97$
Vậy vào năm 2046 thì tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/ năm.
Câu 3. Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen $\left( {mg/l} \right)$ trong một hồ nước sau $t$ giờ $\left( {t \geqslant 0} \right)$ khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
$y\left( t \right) = 5 – \frac{{15t}}{{9{t^2} + 1}}$
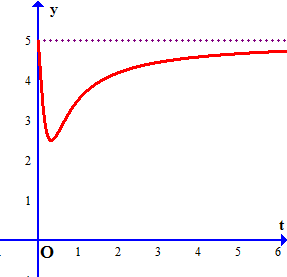
a) Vào thời điểm $t = 1$ thì nồng độ oxygen trong nước là $3,5\left( {mg/l} \right)$
b) Nồng độ oxygen $\left( {mg/l} \right)$ trong một hồ nước không vượt quá $5\left( {mg/l} \right)$
c) Vào thời điểm $t = 0$ thì nồng độ oxygen trong nước cao nhất
d) Nồng độ oxygen $\left( {mg/l} \right)$ trong một hồ nước thấp nhất là $3,5\left( {mg/l} \right)$
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
Xét $y\left( t \right) = 5 – \frac{{15t}}{{9{t^2} + 1}}$ trên nửa đoạn $\left[ {0; + \infty } \right)$
$y’\left( t \right) = \frac{{135{t^2} – 15}}{{{{\left( {9{t^2} + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{1}{3}} \\
{x = – \frac{1}{3}\left( {\;loại\;} \right)}
\end{array}} \right.$
Bảng biến thiên:
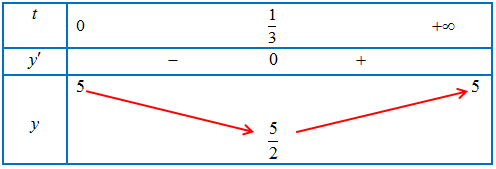
Từ bảng biến thiên, ta thấy và $\mathop {max}\limits_{\left[ {0; + \infty } \right)} y\left( t \right) = y\left( 0 \right) = 5$
Vậy vào các thời điểm $t = 0$ thì nồng độ oxygen trong nước cao nhất và $t = \frac{1}{3}$ giờ thì nồng độ oxygen trong nước thấp nhất.
Câu 4. Xét một chất điểm chuyển động dọc theo trục $Ox$. Toạ độ của chất điểm tại thời điểm $t$ được xác định bởi hàm số $x\left( t \right) = {t^3} – 6{t^2} + 9t$ với $t \geqslant 0$. Khi đó $x’\left( t \right)$ là vận tốc của chất điểm tại thời điểm $t$, kí hiệu $v\left( t \right);v’\left( t \right)$ là gia tốc chuyển động của chất điểm tại thời điểm $t$, kí hiệu $a\left( t \right)$.
a) Hàm $v\left( t \right) = 3{t^2} – 12t + 9$
b) Hàm $a\left( t \right) = 6t – 12$
c) Trong khoảng từ $t = 0$ đến $t = 2$ thì vận tốc của chất điểm tăng
d) Từ $t = 2$ trở đi thì vận tốc của chất điểm giảm
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
a) Hàm $v\left( t \right) = x’\left( t \right) = 3{t^2} – 12t + 9$
b) Hàm $a\left( t \right) = v’\left( t \right) = 6t – 12$
c) d) Tập xác định: $D = \left[ {0; + \infty } \right]$
$a\left( t \right) = 0 \Leftrightarrow t = 2$
Bảng biến thiên:
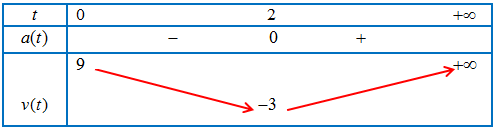
Vậy trong khoảng từ $t = 0$ đến $t = 2$ thì vận tốc của chất điểm giảm, từ $t = 2$ trở đi thì vận tốc của chất điểm tăng
Câu 5. Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho toạ độ của hạt (đơn vị: mét) tại thời điểm $t$ (giây) là $y = {t^3} – 12t + 3,t \geqslant 0$.
a) Hàm vận tốc là: $v\left( t \right) = 3{t^2} – 12,t \geqslant 0$
b) Hạt chuyển động xuống dưới khi $t > 2$
c) Quãng đường hạt đi được trong khoảng thời gian $0 \leqslant t \leqslant 3$ là $9m$
d) Khi $t > 0$ thì hạt tăng tốc
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Đúng |
a) Hàm vận tốc là: $v\left( t \right) = y’ = 3{t^2} – 12,t \geqslant 0$
Hàm gia tốc là: $a\left( t \right) = v’\left( t \right) = y” = 6t,t \geqslant 0$
b) Hạt chuyển động lên trên khi $v\left( t \right) > 0 \Leftrightarrow 3{t^2} – 12 > 0 \Leftrightarrow t > 2$ (do $t \geqslant 0$ )
Hạt chuyển động xuống dưới khi $v\left( t \right) < 0 \Leftrightarrow 3{t^2} – 12 < 0 \Leftrightarrow 0 \leqslant t < 2$ (do $t \geqslant 0$ )
c) Ta có: $y\left( 3 \right) – y\left( 0 \right) = {3^3} – 12.3 + 3 – 3 = – 9$
Vậy quãng đường vật đi được trong thời gian $0 \leqslant t \leqslant 3$ là $9m$.
d) Hạt tăng tốc khi $v\left( t \right)$ tăng hay $v’\left( t \right) > 0$. Do đó, $6t > 0 \Leftrightarrow t > 0$
Hạt giảm tốc khi $v\left( t \right)$ giảm hay $v’\left( t \right) < 0 \Leftrightarrow 6t < 0 \Leftrightarrow t < 0$ (không thỏa mãn do $t \geqslant 0$ )
Câu 6. Một nhà sản xuất trung bình bán được 1000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tằng thêm khoảng 100 ti vi mỗi tuần.
a) Gọi $p$ (triệu đồng) là giá của mỗi ti vi, $x$ là số ti vi. Vậy hàm cầu là: $p\left( x \right) = – \frac{1}{{200}}x + 19$
b) Công ty giảm giá 4,5 (triệu đồng)/1 tivi cho người mua thì doanh thu của công ty là lớn nhất
c) Nếu hàm chi phí hằng tuần là $C\left( x \right) = 12000 – 3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, vậy có 2300 ti vi được bán ra thì lợi nhuận là cao nhất.
d) Nếu hàm chi phí hằng tuần là $C\left( x \right) = 12000 – 3x$ (triệu đồng), trong đó $x$ là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán 8,5 triệu đồng/1 ti vi để lợi nhuận là lớn nhất
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
a) Gọi $p$ (triệu đồng) là giá của mỗi ti vi, $x$ là số ti vi. Khi đó, hàm cầu là $p = p\left( x \right)$.
Theo giả thiết, tốc độ thay đổi của $x$ tỉ lệ với tốc độ thay đổi của $p$ nên hàm số $p = p\left( x \right)$ là hàm số bậc nhất nên. Do đó, $p\left( x \right) = ax + b(a$ khác 0$)$.
Giá tiền ${p_1} = 14$ ứng với ${x_1} = 1000$, giá tiền ${p_2} = 13,5$ ứng với ${x_2} = 1000 + 100 = 1100$
Do đó, phương trình đường thẳng $p\left( x \right) = ax + b$ đi qua hai điểm $\left( {1000;14} \right)$ và $\left( {1100;13,5} \right)$. Ta có hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}
{14 = 1000a + b} \\
{13,5 = 1100a + b}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = \frac{{ – 1}}{{200}}} \\
{b = 19}
\end{array}} \right.$ (thỏa mãn)
Vậy hàm cầu là: $p\left( x \right) = – \frac{1}{{200}}x + 19$
b) Vì $p = \frac{{ – 1}}{{200}}x + 19 \Rightarrow x = – 200p + 3800$
Hàm doanh thu từ tiền bán ti vi là: $R\left( p \right) = px = p\left( { – 200p + 3800} \right)$$ = – 200{p^2} + 3800p$
Để doanh thu là lớn nhất thì ta cần tìm $p$ sao cho $R$ đạt giá trị lớn nhất.
Ta có: $R’\left( p \right) = – 400p + 3800$, $R’\left( p \right) = 0 \Leftrightarrow p = \frac{{19}}{2}$
Bảng biến thiên:
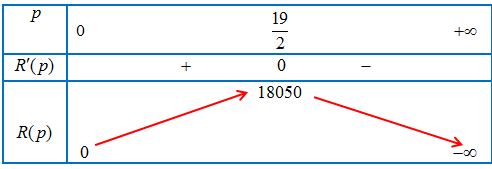
Vậy công ty nên giảm giá số tiền một chiếc ti vi là: $14 – \frac{{19}}{2} = 4,5$ (triệu đồng) thì doanh thu là lớn nhất.
c) Doanh thu bán hàng của $x$ sản phẩm là: $R\left( x \right) = x \cdot p\left( x \right) = x \cdot \left( {\frac{{ – 1}}{{200}}x + 19} \right) = \frac{{ – {x^2}}}{{200}} + 19x$ (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán $x$ sản phẩm là:
$P\left( x \right) = R\left( x \right) – C\left( x \right) = \frac{{ – {x^2}}}{{200}} + 19x – 12000 + 3x = \frac{{ – {x^2}}}{{200}} + 22x – 12000$ (triệu đồng).
Để lợi nhuận là lớn nhất thì $P\left( x \right)$ là lớn nhất.
Ta có: $P’\left( x \right) = \frac{{ – x}}{{100}} + 22,P’\left( x \right) = 0 \Leftrightarrow x = 2200$
Bảng biến thiên:

c) Vậy có 2200 ti vi được bán ra thì lợi nhuận là cao nhất.
Số ti vi mua tăng lên là: $2200 – 1000 = 1200$ (chiếc)
d) Vậy cửa hàng nên đặt giá bán là: $14 – 0,5 \cdot \frac{{1200}}{{100}} = 8$ (triệu đồng)
Câu 7. Một hộ làm nghề dệt vải lụa tơ tằm sản xuất mỗi ngày được $x$ mét vải lụa $\left( {1 \leqslant x \leqslant 18} \right)$. Tổng chi phí sản xuất $x$ mét vải lụa, tính bằng nghìn đồng, cho bởi hàm chi phí:
$C\left( x \right) = {x^3} – 3{x^2} – 20x + 500$. Giả sử hộ làm nghề dệt này bán hết sản phẩm mỗi ngày với giá 220 nghìn đồng/mét. Gọi $B\left( x \right)$ là số tiền bán được và $L\left( x \right)$ là lợi nhuận thu được khi bán $x$ mét vải lụa.
a) Biểu thức tính $B\left( x \right)$ theo $x$ là $B\left( x \right) = 220x$ (nghìn đồng).
b) Biểu thức tính $L\left( x \right)$ theo $x$ là $L\left( x \right) = – {x^3} + 3{x^2} + 220x – 500$ (nghìn đồng).
c) Hộ làm nghề dệt này cần sản xuất và bán ra mỗi ngày 10 mét vải lụa để thu được lợi nhuận tối đa
d) Lợi nhuận tối đa của hộ làm nghề dệt vải lụa tơ tằm có thể đạt được là 1000 nghìn đồng.
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
Khi bán $x$ mét vải lụa:
a) – Số tiền thu được là: $B\left( x \right) = 220x$ (nghìn đồng).
b) – Lợi nhuận thu được là: $L\left( x \right) = B\left( x \right) – C\left( x \right) = – {x^3} + 3{x^2} + 240x – 500$ (nghìn đồng).
c) d) Hàm số $L\left( x \right)$ xác định trên $\left[ {1;18} \right]$.
$L’\left( x \right) = – 3{x^2} + 6x + 240$; $L’\left( x \right) = 0 \Leftrightarrow x = 10$ hoặc $x = – 8$ (loại).
Bảng biến thiên:
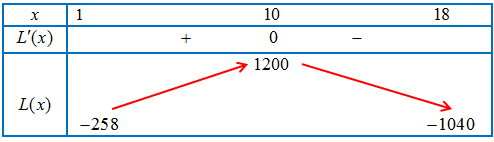
Vậy khi $x = 10$ thì hàm số đạt giá trị lớn nhất là 1200 . Như vậy, hộ làm nghề dệt cần sản xuất và bán ra mỗi ngày 10 mét vải lụa để thu được lợi nhuận tối đa. Lợi nhuận tối đa này là 1200 nghìn đồng.
Câu 8. Giả sử hàm cầu của một sản phẩm độc quyền được cho bởi $P = 400 – 2Q$ và hàm chi phí trung bình $\overline C = 0,2Q + 4 + \frac{{400}}{Q}$ trong đó $Q$ là số đơn vị sản phẩm $(P$ và $\overline C $ được tính bằng $\$ $ đối với mỗi đơn vị sản phẩm).
a) $Q = 90$ là lượng sản phẩm bán ra để lợi nhuận thu được tối đa;
b) Giá bán để lợi nhuận thu được tối đa là $400\$ $
c) Lợi nhuận tối đa là $17420\$ $
d) Nếu chính phủ đánh thuế $22\$ $ / một đơn vị sản phẩm thì giá bán $390\$ $ để lợi nhuận thu được tối đa
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
Ta có Lợi nhuận = Tổng doanh thu – Tổng chi phí.
Tổng doanh thu là $R$ và tổng chi phí là $C$ được cho bởi $R = PQ = 400Q – 2{Q^2}$
Và $C = Q\overline C = 0,2{Q^2} + 4Q + 400$, nên lợi nhuận
$P = R – C = 400Q – 2{Q^2} – \left( {0,2{Q^2} + 4Q + 400} \right)$.
Hay $P\left( Q \right) = 396Q – 2,2{Q^2} – 400$.
a) Để tối đa hóa lợi nhuận, ta cho $P’\left( Q \right) = 0 \Leftrightarrow 396 – 4,4Q = 0 \Leftrightarrow Q = 90$.
Ta có $P”\left( Q \right) = – 4,4 < 0$.
Vậy $P$ đạt cực đại tại $Q = 90$.
b) Thay $Q = 90$ vào hàm cầu ta được giá bán trên mỗi sản phẩm để lợi nhuận thu được tối đa: $P = 400 – 2\left( {90} \right) = 220$.
c) Lợi nhuận tối đa $P\left( {90} \right) = 396\left( {90} \right) – 2,2{(90)^2} – 400 = 17420$.
d) Khi chi phí đánh thuế $22\$ /$ một đơn vị sản phẩm, tổng chi phí tăng $22Q$. Hàm chi phí mới là $\overline {{C_1}} = 0,2{Q^2} + 4Q + 400 + 22Q$ và hàm lợi nhuận mới là
${P_1} = 400Q – 2{Q^2} – \left( {0,2{Q^2} + 4Q + 400 + 22Q} \right)$
$ = 374Q – 2,2{Q^2} – 400$
Ta có $P_1’\left( Q \right) = 0 \Leftrightarrow 374 – 4,4Q = 0 \Leftrightarrow Q = 85$.
Vì $P_1{”}\left( Q \right) = – 4,4 < 0$ nên để thu được lợi nhuận tối đa, nhà độc quyền phải sản xuất 85 đơn vị sản phẩm với mức giá ${P_1} = 400 – 2\left( {85} \right) = 230\$ $, do mức giá này chỉ hơn $10\$ $ so với trước đó nên chỉ một phần thuế được tính vào người tiêu dùng, phần thuế còn lại do nhà sản xuất gánh chịu. Lợi nhuận bây giờ là 15495 .
Câu 9. Một sợi dây kim loại dài $a\left( {\;cm} \right)$. Người ta cắt đoạn dây đó thành hai đoạn. Đoạn có độ dài $x$ $\left( {cm} \right)$ được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông $(a > x > 0)$.
a) Bán kính đường tròn: $r = \frac{x}{\pi }$.
b) Diện tích hình vuông: ${\left( {\frac{{a – x}}{4}} \right)^2}$.
c) Tổng diện tích hai hình: $\frac{{\left( {4 + \pi } \right) \cdot {x^2} – 2a\pi x + \pi {a^2}}}{{16\pi }}$.
d) Khi $x = \frac{{a\pi }}{{2 + \pi }}$ thì hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
Lời giải
| a) Sai | b) Đúng | c) Đúng | d) Sai |
Do $x$ là độ dài của đoạn dây cuộn thành hình tròn $(0 < x < a)$.
Suy ra chiều dài đoạn còn lại là $a – x$.
Chu vi đường tròn: $2\pi r = x \Rightarrow r = \frac{x}{{2\pi }}$.
Diện tích hình tròn: ${S_1} = \pi \cdot {r^2} = \frac{{{x^2}}}{{4\pi }}$.
Diện tích hình vuông: ${S_2} = {\left( {\frac{{a – x}}{4}} \right)^2}$.
Tổng diện tích hai hình: $S = \frac{{{x^2}}}{{4\pi }} + {\left( {\frac{{a – x}}{4}} \right)^2} = \frac{{\left( {4 + \pi } \right) \cdot {x^2} – 2a\pi x + \pi {a^2}}}{{16\pi }}$.
Đạo hàm: $S’ = \frac{{\left( {4 + \pi } \right) \cdot x – a\pi }}{{8\pi }}$;
$S’ = 0 \Leftrightarrow x = \frac{{a\pi }}{{4 + \pi }}$
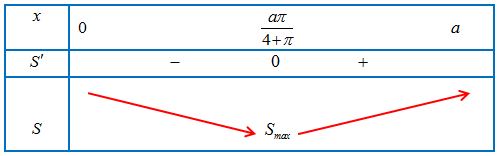
Vậy $S$ đạt giá trị nhỏ nhất tại $x = \frac{{a\pi }}{{4 + \pi }}$.
Câu 10. Một người đàn ông muốn chèo thuyền ở vị trí $A$ tới điểm $B$ về phía hạ lưu bờ đối diện, càng nhậnh càng tốt, trên một bờ sông thẳng rộng 3 km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến $C$ và sau đó chạy đến $B$, hay có thể chèo trực tiếp đến $B$, hoặc anh ta có thể chèo thuyền đến một điểm $D$ giữa $C$ và $B$ và sau đó chạy đến $B$. Biết anh ấy có thể chèo thuyền $6\;km/h$, chạy $8\;km/h$ và quãng đường $BC = 8\;km$. Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông.
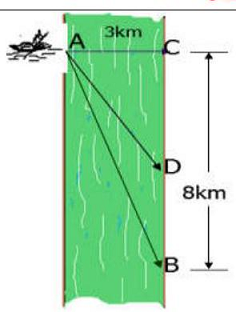
Gọi $x\left( {\;km} \right)$ là độ dài quãng đường $BD$. Khi đó:
a) $8 – x\left( {\;km} \right)$ là độ dài quãng đường $CD$.
b) Thời gian chèo thuyền trên quãng đường $AD$ là: $\frac{{\sqrt {{x^2} + 9} }}{3}$ (giờ)
c) Tổng thời gian di chuyển từ $A$ đến $B$ là $\frac{{\sqrt {{x^2} + 9} }}{3} + \frac{{8 – x}}{8}$
d) Khoảng ${1^h}{20′}$ là khoảng thời gian ngắn nhất để người đàn ông đến $B$.
Lời giải
| a) Đúng | b) Sai | c) Sai | d) Đúng |
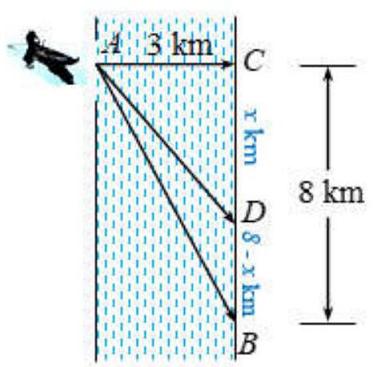
Gọi $x\left( {\;km} \right)$ là độ dài quãng đường $BD;8 – x\left( {\;km} \right)$ là độ dài quãng đường $CD$.
Thời gian chèo thuyền trên quãng đường $AD = \sqrt {{x^2} + 9} $ là: $\frac{{\sqrt {{x^2} + 9} }}{6}$ (giờ)
Thời gian chạy trên quãng đường $DB$ là: $\frac{{8 – x}}{8}$ (giờ)
Tổng thời gian di chuyển từ $A$ đến $B$ là $f\left( x \right) = \frac{{\sqrt {{x^2} + 9} }}{6} + \frac{{8 – x}}{8}$
Xét hàm số $f\left( x \right) = \frac{{\sqrt {{x^2} + 9} }}{6} + \frac{{8 – x}}{8}$ trên khoảng $\left( {0;8} \right)$
Ta có $f’\left( x \right) = \frac{x}{{6\sqrt {{x^2} + 9} }} – \frac{1}{8};f’\left( x \right) = 0 \Leftrightarrow 3\sqrt {{x^2} + 9} = 4x \Leftrightarrow x = \frac{9}{{\sqrt 7 }}$
Bảng biến thiên
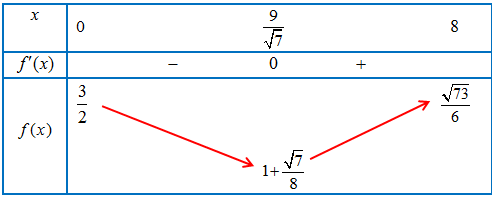
Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ $A$ đến $B$ là $1 + \frac{{\sqrt 7 }}{8} \approx {1^h}{20′}$.
Vậy khoảng thời gian ngắn nhất để người đàn ông đến $B$ là $1 + \frac{{\sqrt 7 }}{8} \approx {1^h}{20′}$.
Câu 11. Từ một tấm bìa hình vuông $ABCD$ có cạnh $50\,cm$,
người ta cắt bỏ bốn tam giác cân bằng nhau là $AMB$, $BNC$, $CPD$ và $DQA$ Với phần còn lại, người ta gấp lên và ghép lại thành hình chóp tứ giác đều.
Gọi cạnh đáy của mô hình là $x\left( {\;cm} \right)$ với $x > 0$. Khi đó :
a) Chiều cao của hình chóp là $\sqrt {1250 – 25\sqrt 2 x} $.
b) Điều kiện của $x$ là: $0 < x < 25\sqrt 2 $
c) Thể tích của khối chóp bằng $\frac{1}{3} \cdot \sqrt {1250{x^3} – 25\sqrt 2 {x^4}} $.
d) Cạnh đáy của khối chóp bằng $3\sqrt 2 \,dm$ thì thể tích của khối chóp là lớn nhất.
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
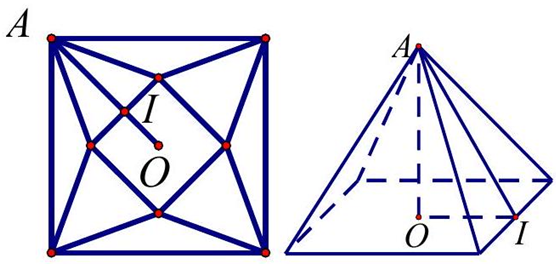
Gọi cạnh đáy của mô hình là $x\left( {\;cm} \right)$ với $x > 0$. Ta có $AI = AO – IO = 25\sqrt 2 – \frac{x}{2}$.
Chiều cao của hình chóp $h = \sqrt {A{I^2} – O{I^2}} = \sqrt {{{\left( {25\sqrt 2 – \frac{x}{2}} \right)}^2} – {{\left( {\frac{x}{2}} \right)}^2}} = \sqrt {1250 – 25\sqrt 2 x} $.
Thể tích của khối chóp bằng $V = \frac{1}{3} \cdot {x^2} \cdot \sqrt {1250 – 25\sqrt 2 x} $
$ = \frac{1}{3} \cdot \sqrt {1250{x^4} – 25\sqrt 2 {x^5}} $.
Điều kiện $1250 – 25\sqrt 2 x > 0 \Rightarrow x < 25\sqrt 2 $.
Xét hàm số $y = \frac{1}{3} \cdot \sqrt {1250{x^4} – 25\sqrt 2 {x^5}} $ với $0 < x < 25\sqrt 2 $.
Ta có $y’ = \frac{1}{3} \cdot \frac{{5000{x^3} – 125\sqrt 2 {x^4}}}{{2\sqrt {1250{x^4} – 25\sqrt 2 {x^3}} }}$.
Có $y’ = 0 \Rightarrow 5000{x^3} – 125\sqrt 2 {x^4} = 0 \Rightarrow x = 20\sqrt 2 $.
Bảng biến thiên

Vậy để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình bằng $20\sqrt 2 \,cm = 2\sqrt 2 \,dm$
Câu 12. Một ngọn hải đăng được đặt tại vị trí $A$ cách bờ biển một khoảng $AB = 5\;km$. Trên bờ biển có một cái kho ở vị trí $C$ cách $B$ một khoảng $BC = 7\;km$ (tham khảo hình vẽ).
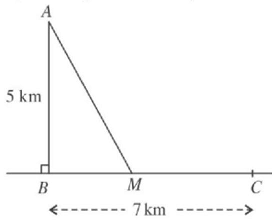
Người canh hải đăng có thể chèo đò từ vị trí $A$ đến vị trí $M$ trên bờ biển với vận tốc $4\;km/h$ và đi bộ đến kho $C$ với vận tốc $6\;km/h$.
Đặt $BM = x$ với $0 < x < 7$. Khi đó:
a) Thời gian đi từ $A$ đến $M$ là $\frac{{\sqrt {25 + {x^2}} }}{4}$.
b) Thời gian đi từ $A$ đến $C$ là $\frac{{\sqrt {25 + {x^2}} }}{4} + \frac{{7 – x}}{6}$.
c) Thời gian ngắn nhất từ $A$ đến $C$ là khoảng $3h06$ phút.
d) Muộn nhất $3h54$ phút người đó phải xuất phát từ vị trí $A$ để có mặt tại kho $C$ lúc 7 giờ sáng
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Sai |
Thời gian đi từ $A$ đến $M$ là $\frac{{\sqrt {25 + {x^2}} }}{4}$.
Thời gian đi từ $M$ đến $C$ là $\frac{{7 – x}}{6}$.
Tổng thời gian đi từ $A$ đến $C$ là $\frac{{\sqrt {25 + {x^2}} }}{4} + \frac{{7 – x}}{6}$.
Xét hàm số $f\left( x \right) = \frac{{\sqrt {25 + {x^2}} }}{4} + \frac{{7 – x}}{6}$.
Ta có $f’\left( x \right) = \frac{x}{{4\sqrt {25 + {x^2}} }} – \frac{1}{6};f’\left( x \right) = 0 \Leftrightarrow \frac{x}{{4\sqrt {25 + {x^2}} }} – \frac{1}{6} = 0 \Leftrightarrow 2\sqrt {25 + {x^2}} = 3x \Leftrightarrow x = 2\sqrt 5 $.
Bảng biến thiên
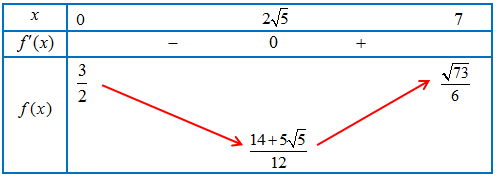
Thời gian ngắn nhất là $t = \frac{{14 + 5\sqrt 5 }}{{12}} = 2,098 \Rightarrow t \approx 2h06$ phút.
Vậy người đó xuất phát muộn nhất lúc $4h54$ phút.
Câu 13. Ông Nam cần xây dựng một bể chứa nước có dạng hình hộp chữ nhật không có nắp đậy để phục vụ cho việc tưới cây trong vườn. Do các điều kiện về diện tích vườn, ông Nam cần bể có thể tích là $36\;{m^3}$, đáy bể có chiều dài gấp hai lần chiều rộng và chiều rộng không quá 4 m , biết rằng chi phí vật liệu xây dựng mỗi mét vuông diện tích bề mặt là như nhau.
Gọi $x\left( m \right)$ là chiều rộng của bể, ta có $0 < x \leqslant 4$. Khi đó
a) Chiều dài của bể là $2x\left( {\;m} \right)$
b) Chiều cao của bể là $\frac{{18}}{{{x^2}}}\left( m \right)$.
c) Tổng diện tích các mặt cần xây là: $2{x^2} + \frac{{108}}{x}$.
d) Chiều cao bể nước bằng $3\left( {\;m} \right)$ thì tổng chi phí vật liệu là nhỏ nhất
Lời giải
| a) Đúng | b) Đúng | c) Đúng | d) Sai |
Xem bể chứa có dạng hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ như Hình.
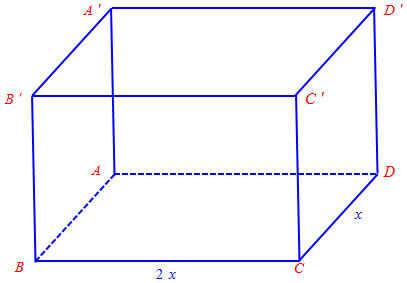
Chiều dài của bể là $2x\left( m \right)$.
Gọi $h\left( m \right)$ là chiều cao bể nước, ta có thể tích của bể là $V = x \cdot \left( {2x} \right) \cdot h$.
Suy ra $h = \frac{V}{{2{x^2}}} = \frac{{36}}{{2{x^2}}} = \frac{{18}}{{{x^2}}}\left( m \right)$.
Tổng diện tích các mặt cần xây là:
$S = {S_{ABCD}} + 2 \cdot {S_{ABB’A’}} + 2 \cdot {S_{BCC’B’}}$
$ = 2{x^2} + 2.x \cdot \frac{{18}}{{{x^2}}} + 2.2x \cdot \frac{{18}}{{{x^2}}} = 2{x^2} + \frac{{108}}{x}$
Xét hàm số $S\left( x \right) = 2{x^2} + \frac{{108}}{x}(0 < x \leqslant 4)$, ta có:
$S’\left( x \right) = 4x – \frac{{108}}{{{x^2}}} = $
$\frac{{4{x^3} – 108}}{{{x^2}}} = \frac{{4\left( {x – 3} \right)\left( {{x^2} + 3x + 9} \right)}}{{{x^2}}}$.
$S’\left( x \right) = 0 \Leftrightarrow x = 3$.
Do ${x^2} > 0$ và ${x^2} + 3x + 9 > 0$ khi $x \in \left( {0;4} \right]$ nên dấu của $S’\left( x \right)$ trên $\left( {0;4} \right]$ phụ thuộc dấu của biểu thức $x – 3$.
Bảng biến thiên:
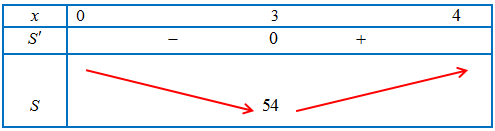
Chi phí vật liệu xây dựng thấp nhất khi tổng diện tích các mặt cần xây $S\left( x \right)$ là nhỏ nhất. Dựa vào bảng biến thiên, ta có $S\left( x \right)$ đạt giá trị nhỏ nhất tại $x = 3$, suy ra $h = 2$.
Vậy cần xây bể có chiều cao là $2\left( {\;m} \right)$.
Câu 14. Một tấm kẽm hình vuông $ABCD$ có cạnh bằng 30 cm . Người ta gập tấm kẽm theo hai cạnh $EF$ và $GH$ cho đến khi $AD$ và $BC$ trùng nhau như hình vẽ bên để được một hình lăng trụ khuyết hai đáy.
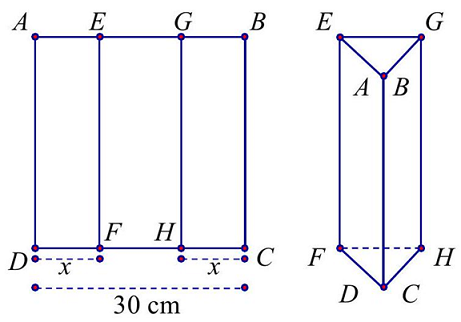
Khi đó:
a) Thể tích khối trụ được tính bằng công thức $V = 30S$ trong đó $S$ là diện tích của tam giác $AEG$.
b) Diện tích của tam giác $AEG$ bằng: $\sqrt {30} \cdot \sqrt {{{(15 – x)}^2}\left( {2x – 15} \right)} $
c) Giá trị của $x$ để thể tích khối lăng trụ lớn nhất là $x = 10\left( {\;cm} \right)$
d) Thể tích khối lăng trụ lớn nhất bằng 1250
Lời giải
| a) Đúng | b) Sai | c) Đúng | d) Sai |
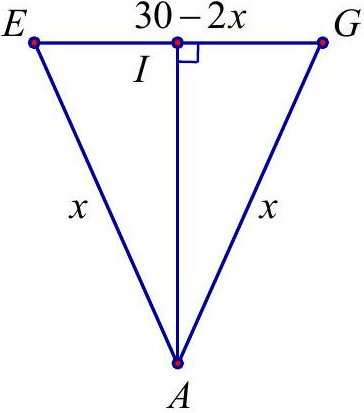
Đường cao lăng trụ là $AD = AB = 30\;cm$ không đổi. Để thể tích lăng trụ lớn nhất chỉ cần diện tích đáy lớn nhất.
Gọi $I$ là trung điểm cạnh $EG \Rightarrow AI \bot EG$ trong tam giác $AEG$.
Khi đó $IG = 15 – x,(0 < x < 15)$
Có $AI = \sqrt {{x^2} – {{\left( {\frac{{30 – 2x}}{2}} \right)}^2}} = \sqrt {{x^2} – {{(15 – x)}^2}} $ $ = \sqrt {30x – 225} ,x \in \left( {\frac{{15}}{2};15} \right)$.
${S_{\vartriangle AEG}} = \frac{1}{2}AI \cdot EG = \frac{1}{2}\left( {30 – 2x} \right)\sqrt {30x – 225} $ $ = \sqrt {15} \cdot \sqrt {{{(15 – x)}^2}\left( {2x – 15} \right)} $
Vậy ta cần tìm $x \in \left( {\frac{{15}}{2};15} \right)$ để $f\left( x \right) = {(15 – x)^2}\left( {2x – 15} \right)$ lớn nhất.
$f’\left( x \right) = – 2\left( {15 – x} \right)\left( {2x – 15} \right) + 2{(15 – x)^2}$
$ = 2\left( {15 – x} \right)\left( {30 – 3x} \right) = 0$
$f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 15} \\
{x = 10}
\end{array}} \right.$.
Bảng biến thiên:
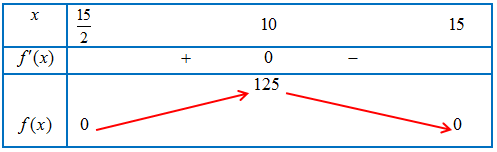
Vậy thể tích lăng trụ lớn nhất khi $x = 10$.
Và thể tích lớn nhất bằng $125.30 = 3750\left( {\;c{m^3}} \right)$
Câu 15. Bác thợ hàn dùng một thanh kim loại dài 250 cm để uốn thành khung cửa sổ có dạng như hình vẽ. Gọi $r$ là bán kính của nửa đường tròn,
a) Diện tích của nửa hình tròn là ${S_1} = \frac{1}{2}\pi {r^2}$
b) Diện tích của hình chữ nhật là ${S_2} = 250r – \pi {r^2} – 2{r^2}$
c) Khi $r = 10$ thì giá trị diện tích của khung cửa sổ nằm trong khoảng $\left( {2000;2140} \right)$
d) Biết $r = {r_0}$ thì diện tích tạo thành đạt giá trị lớn nhất khi đó ${r_0} \in \left( {35;36} \right)$
Lời giải
| a) Đúng | b) Đúng | c) Sai | d) Đúng |
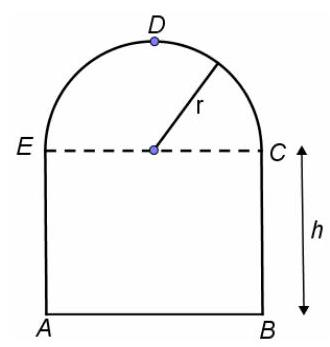
Gọi ${S_1},{S_2}$ lần lượt là diện tích của nửa hình tròn và hình chữ nhật. Khi đó:
${S_1} = \frac{1}{2}\pi {r^2};{S_2} = 2rh$; với $2h = 250 – \left( {\pi r + 2r} \right)$ nên ${S_2} = 250r – \pi {r^2} – 2{r^2}$.
Suy ra diện tích hình cần tìm $S = \frac{1}{2}\pi {r^2} + 250r – \pi {r^2} – 2{r^2} = – \frac{1}{2}\pi {r^2} – 2{r^2} + 250r$.
Bài toán trở thành tìm giá trị lớn nhất của hàm số $S\left( r \right) = – \frac{1}{2}\pi {r^2} – 2{r^2} + 250r$ với $0 < r < 125$.
Ta có $S’\left( r \right) = – \left( {\pi + 4} \right)r + 250;S’\left( r \right) = 0 \Leftrightarrow r = \frac{{250}}{{\pi + 4}}$.
Đây là cực trị duy nhất của hàm số đồng thời $S’\left( r \right)$ đổi dấu từ dương sang âm khi $r$ qua $\frac{{250}}{{\pi + 4}}$ nên hàm số đạt giá trị lớn nhất tại điểm này.
———-
Để lại một bình luận