Ứng Dụng Hệ Tọa Độ Không Gian Oxyz Để Giải Các Bài Toán Hình Học – Toán 12

Ứng dụng hệ tọa độ không gian oxyz để giải các bài toán hình học giải chi tiết được soạn dưới dạng file word và PDF gồm 8 trang. Các bạn xem và tải về ở dưới.

A. PHƯƠNG PHÁP

I. Gắn tọa độ đối với hình chóp

1. Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:

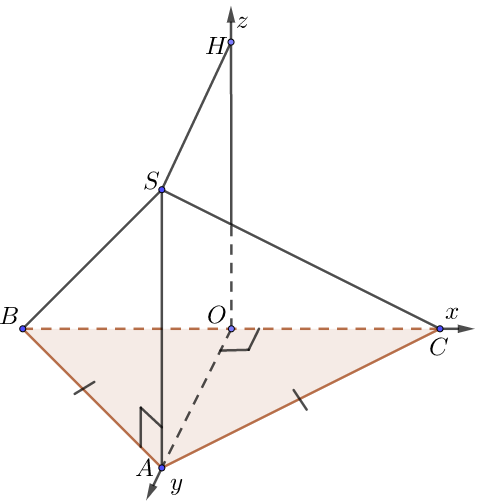
a) Đáy là tam giác đều

• Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ, $AB = a = 1$.

• Tọa độ các điểm là: $O(0;0;0),\,\,A\left( {0;\frac{{\sqrt 3 }}{2};0} \right)$, $B\left( { – \frac{1}{2};0;0} \right)$, $C\left( {\frac{1}{2};0;0} \right)$, $S\left( {0;\frac{{\sqrt 3 }}{2};\underbrace {OH}_{ = SA}} \right)$

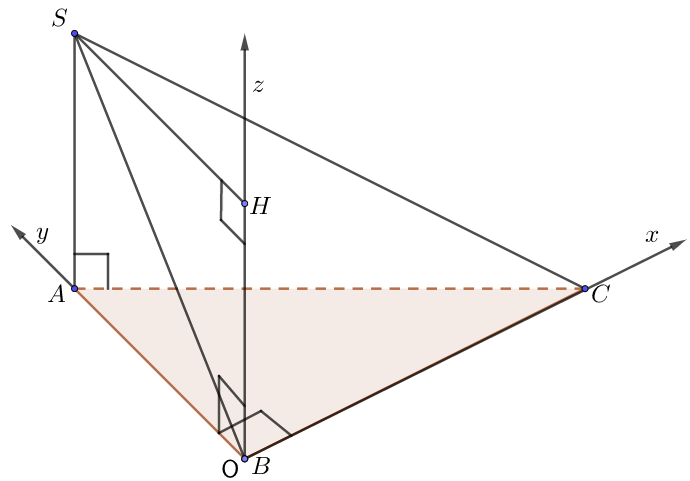
b) Đáy là tam giác cân tại A

• Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm là: $O(0;0;0)$, $A\left( {0;OA;0} \right)$, $B\left( { – OB;0;0} \right)$, $C\left( {OC;0;0} \right)$, $S\left( {0;OA;\underbrace {OH}_{ = SA}} \right)$

c) Đáy là tam giác cân tại B

• Gọi O là trung điểm AC. Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $O\left( {0;0;0} \right)$, $A\left( { – OA;0;0} \right)$, $B\left( {0,OB;0} \right)$$C\left( {OC;0;0} \right)$, $S\left( { – OA;0;\underbrace {OH}_{ = SA}} \right)$.

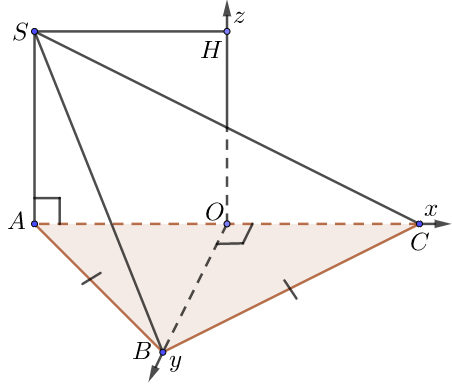
d) Đáy là tam giác vuông tại B

• Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $B \equiv O\left( {0;0;0} \right)$, $C\left( {BC,0;0} \right)$, $A\left( {0;AB;0} \right)$, $S\left( {0;AB;\underbrace {BH}_{ = SA}} \right)$.

e) Đáy là tam giác vuông tại A

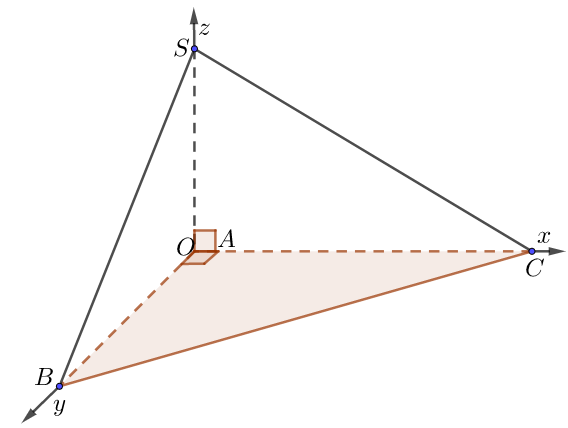
• Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $A \equiv O\left( {0;0;0} \right)$, $B\left( {0;OB;0} \right),\,\,C\left( {AC;0;0} \right),$$S\left( {0;0;SA} \right)$.

e) Đáy là tam giác thường

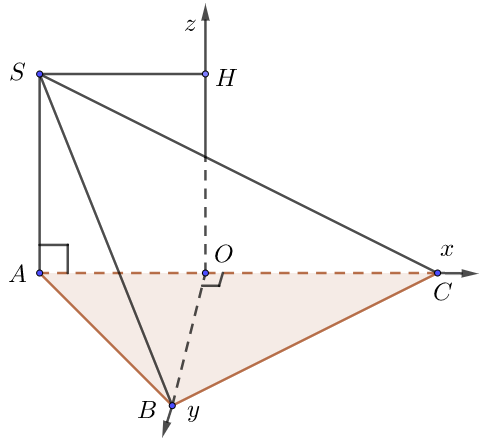
• Dựng đường cao BO của $\Delta ABC.$Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $O\left( {0;0;0} \right)$,

$A\left( { – OA;0;0} \right)$, $B\left( {0,OB;0} \right)$, $C\left( {OC;0;0} \right)$, $S\left( { – OA;0;\underbrace {OH}_{ = SA}} \right)$

f) Đáy hình vuông, hình chữ nhật

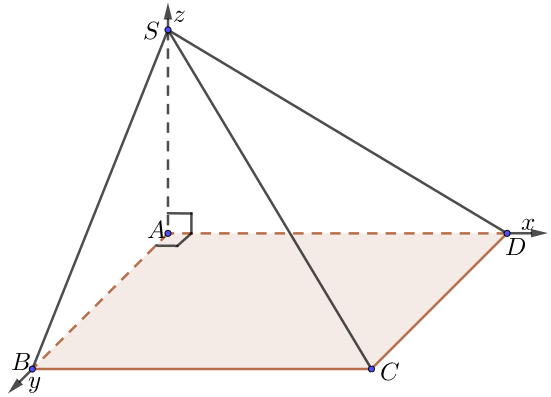
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $A \equiv O\left( {0;0;0} \right)$,$B\left( {0;AB;0} \right),$ $C\left( {AD;AB;0} \right)$, $\,D\left( {AD;0;0} \right)$, $S\left( {0;0;SA} \right)$

g) Đáy là hình thoi

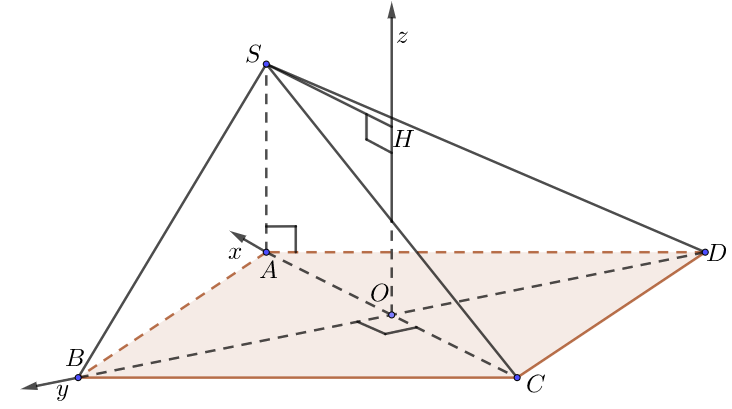
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $O\left( {0;0;0} \right)$, $A\left( {OA;0;0} \right),$ $B\left( {0;OB;0} \right)$,$C\left( { – OC;0;0} \right)$, $D\left( {0; – OD;0} \right)$, $S\left( {OA;0;\underbrace {OH}_{ = SA}} \right)$

h) Đáy là hình thang vuông

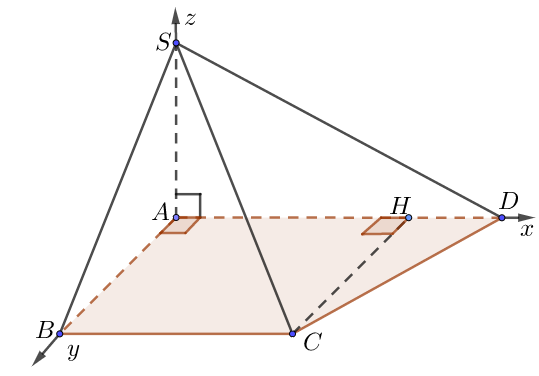
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $A \equiv O\left( {0;0;0} \right)$,$B\left( {0;AB;0} \right),\,\,C\left( {AH;AB;0} \right),$$D\left( {AD;0;0} \right),\,\,S\left( {0;0;SA} \right).$

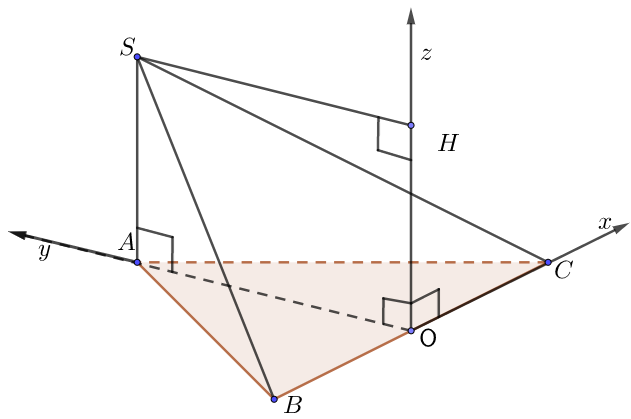
2. Hình chóp có mặt bên (SAB) vuông góc với mặt đáy

a) Đáy là tam giác, mặt bên là tam giác thường

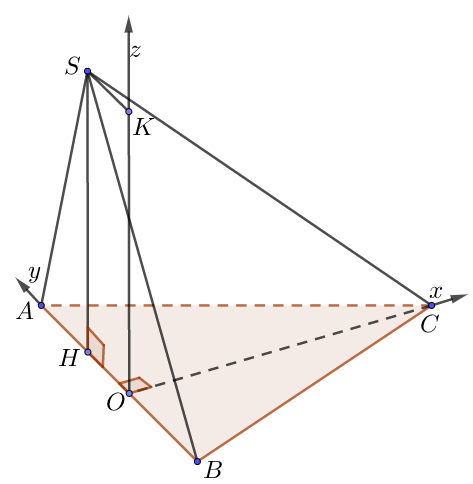
• Vẽ đường cao CO trong $\Delta ABC$. Chọn hệ trục như hình, a = 1.

• Ta có: $O\left( {0;0;0} \right),\,\,A\left( {0;OA;0} \right),$ $B\left( {0; – OB;0} \right)$, $C\left( {OC;0;0} \right)$,$S\left( {0;OH;\underbrace {OK}_{ = SH}} \right)$

b) Đáy là tam giác cân tại C (hoặc đều), mặt bên là tam giác cân tại S (hoặc đều)

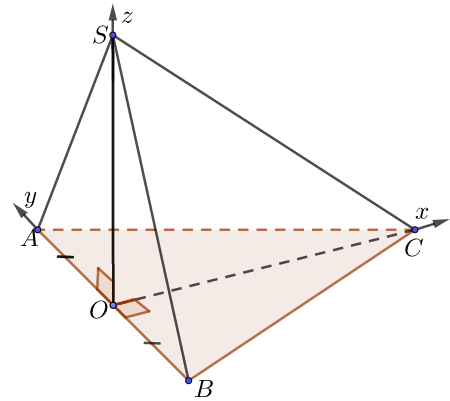
• Gọi O là trung điểm BC, chọn hệ trục như hình, a = 1.

• Ta có: $O\left( {0;0;0} \right),\,\,A\left( {0;OA;0} \right),$

$B\left( {0; – OB;0} \right),\,\,C\left( {OC;0;0} \right),\,\,S\left( {0;0;SO} \right)$

c) Đáy là hình vuông-hình chữ nhật

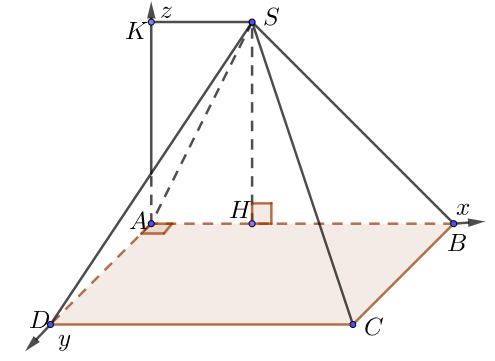
• Dựng hệ trục như hình, chọn a = 1.

• Ta có:

$A \equiv O\left( {0;0;0} \right),\,B\left( {AB;0;0} \right),C\left( {AB;AD;0} \right),\,$ $D\left( {0;AD;0} \right),\,$$S\left( {AH;0;\underbrace {AK}_{ = SH}} \right)$

3. Hình chóp đều

a) Hình chóp tam giác đều

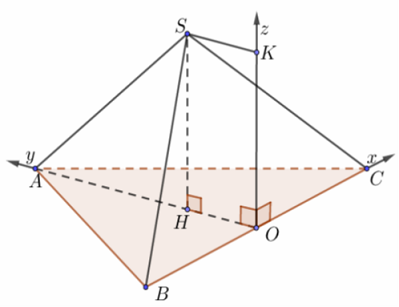
Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như hình vẽ và a = 1.

Tọa độ điểm:

$O\left( {0;0;0} \right),$$A\left( {0;\frac{{AB\sqrt 3 }}{2};0} \right)$,$B\left( { – \frac{{BC}}{2};0;0} \right)$, $C\left( {\frac{{BC}}{2};0;0} \right)$, $S\left( {0;\underbrace {\frac{{AB\sqrt 3 }}{6}}_{ = OH};\underbrace {OK}_{ = SH}} \right)$.

b) Hình chóp tứ giác đều

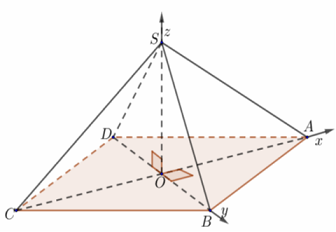
Chọn hệ trục như hình với a = 1.

Tọa độ điểm:

$O\left( {0;0;0} \right),$$A\left( {\underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OA};0;0} \right),$$B\left( {0;\underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OB};0} \right)$,$C\left( {\underbrace { – \frac{{AB\sqrt 2 }}{2}}_{ = – OA};0;0} \right),$ $D\left( {0; – \underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OB};0} \right);$$S\left( {0;0;SO} \right)$.

II. Gắn tọa độ đối với hình lăng trụ

1. Lăng trụ đứng

a) Hình lập phương, hình hộp chữ nhật

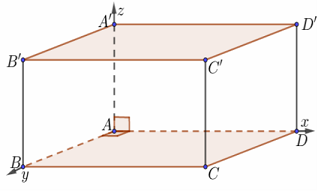
Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:

$A \equiv O\left( {0;0;0} \right),$

$B\left( {0;AB;0} \right),$$C\left( {AD;AB;0} \right)$,

$D\left( {AD;0;0} \right)$,

$A’\left( {0;0;AA’} \right),$

$B’\left( {0;AB;AA’} \right),$$C’\left( {AD;AB;AA’} \right)$, $D’\left( {AD;0;AA’} \right).$

b) Lăng trụ đứng đáy là hình thoi

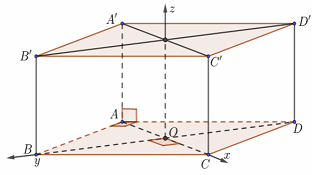
Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình với

$O\left( {0;0;0} \right),$$A\left( { – OA;0;0} \right),$$\,B\left( {0;OB;0} \right),$$\,C\left( {OC;0;0} \right),$$\,D\left( {0; – OD;0} \right),$$\,A’\left( { – OA;0;AA’} \right),$$\,B’\left( {0;OB;AA’} \right),$$\,C’\left( {OC;0;CC’} \right),$$\,D’\left( {0; – OD;DD’} \right)$

c) Lăng trụ tam giác đều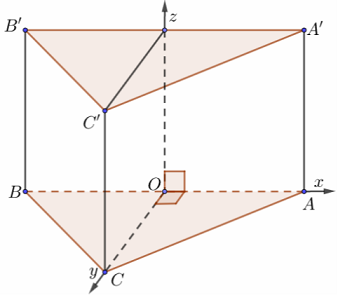

Gọi O là trung điểm một cạnh đáy, chọn hệ trục như hình vẽ với a = 1. Ta có:

$O\left( {0;0;0} \right),$$A\left( {\frac{{AB}}{2};0;0} \right),$$B\left( { – \frac{{AB}}{2};0;0} \right),$$C\left( {0;OC;0} \right),$$A’\left( {OA;0;AA’} \right),$$B’\left( { – \frac{{AB}}{2};0;BB’} \right),$$C’\left( {0;OC;CC’} \right).$

d) Lăng trụ đứng có đáy tam giác thường

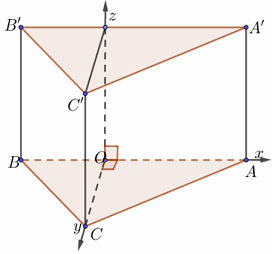
Vẽ đường cao CO trong tam giác ABC và chọn hệ trục như hình vẽ với a = 1.

Tọa độ điểm là:

$O\left( {0;0;0} \right),$$A\left( {OA;0;0} \right),$$B\left( { – OB;0;0} \right),$$C\left( {0;OC;0} \right),$$A’\left( {OA;0;AA’} \right),$$B’\left( { – OB;0;BB’} \right),$$C’\left( {0;OC;CC’} \right).$

2. Lăng trụ xiên:

a) Lăng trụ xiên có đáy là tam giác đều, hình chiếu của đỉnh trên mặt phẳng đối diện là trung điểm một cạnh tam giác đáy

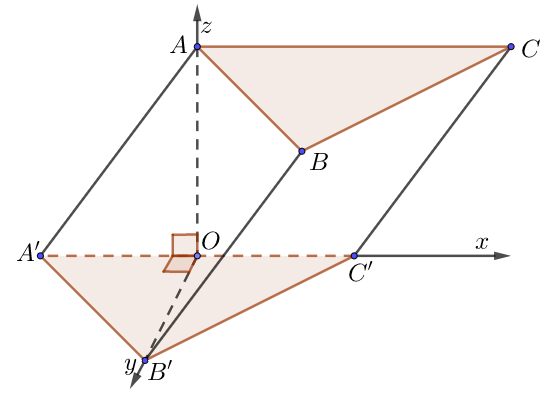
• Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các điểm $O,\,\,A’,\,\,B’,\,\,C’,\,\,A$.

• Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ bằng nhau: $\overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {CC’} $.

b) Lăng trụ xiên có đáy là hình vuông hoặc hình chữ nhật, hình chiếu của một đỉnh là một điểm thuộc cạnh đáy không chứa đỉnh đó

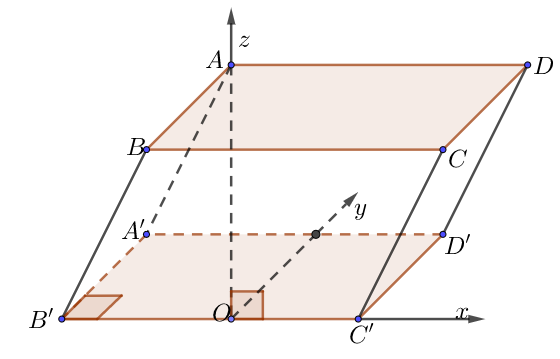
• Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các điểm $O,\,\,A’,\,\,B’,\,\,C’,\,\,D’,\,\,A$.

• Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ bằng nhau: $\overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {CC’} = \overrightarrow {DD’} $.

B. CÁC VÍ DỤ MINH HỌA

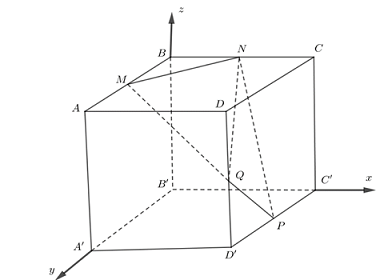
Ví dụ 1. Cho hình lập phương $ABCD.A’B’C’D’$ có độ dài cạnh bằng $1$. Gọi $M,N,P,Q$ lần lượt là trung điểm của $AB,BC,C’D’,DD’$. Chọn hệ tọa độ $Oxyz$ như hình vẽ, xác định tọa độ các điểm $M,N,P,Q$.

Lời giải

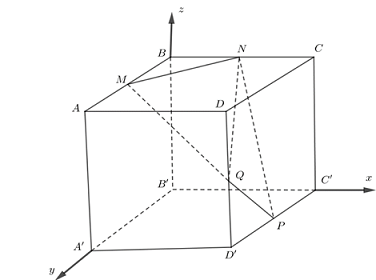
Thiết lập hệ tọa độ $Oxyz$ như hình vẽ, gốc $O \equiv B’$.

Khi đó:$M\left( {0\,;\,\frac{1}{2}\,;\,1} \right)$, $N\left( {\frac{1}{2}\,;\,0\,;\,1} \right)$, $P\left( {1\,;\,\frac{1}{2}\,;\,0} \right)$, $Q\left( {1\,;\,1\,;\,\frac{1}{2}} \right)$.

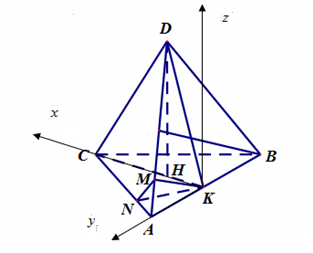
Ví dụ 2. Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $K$ là trung điểm $AB$, gọi $M\,,\,N$ lần lượt là hình chiếu vuông góc của $K$ lên $AD\,,\,AC$. Chọn hệ tọa độ $Oxyz$ như hình vẽ, xác định tọa độ các điểm $K,M,N$ theo $a$.

Lời giải

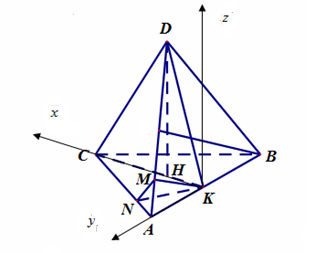
ta có: $KC = \frac{{\sqrt 3 }}{2}a\,;DH = \frac{{\sqrt 6 }}{3}a\,;\,HK = \frac{{\sqrt 3 }}{6}a$.

$AN = \frac{1}{4}AC\,;\,AM = \frac{1}{4}AD$

Chọn hệ trục $Oxyz$ sao cho $K \equiv O\left( {0\,;\,0\,;\,0} \right)$. $A\left( {0\,;\,\frac{a}{2}\,;\,0} \right)$, $\,C\left( {\frac{{a\sqrt 3 }}{2}\,;\,0\,;\,0} \right)$, $D\left( {\frac{{a\sqrt 3 }}{6}\,;\,0\,;\,\frac{{a\sqrt 6 }}{3}} \right)$

Ta có: $\overrightarrow {AN} = \frac{1}{4}\overrightarrow {AC} \Rightarrow N\left( {\frac{{a\sqrt 3 }}{{8\,}};\,\frac{{3a}}{8}\,;\,0} \right)$.

$\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AD} \Rightarrow M\left( {\frac{{a\sqrt 3 }}{{24\,}};\,0\,;\,\frac{{a\sqrt 6 }}{{12\,}}} \right)$

Vậy$K\left( {0\,;\,0\,;\,0} \right),\,M\left( {\frac{{a\sqrt 3 }}{{24\,}};\,0\,;\,\frac{{a\sqrt 6 }}{{12\,}}} \right)$, $N\left( {\frac{{a\sqrt 3 }}{{8\,}};\,\frac{{3a}}{8}\,;\,0} \right)$.

Ví dụ 3. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SAD$ là tam giác đều và nằm trong mặt phẳng với đáy. Gọi $M$ và $N$ lần lượt là trung điểm của $BC$ và $CD$. Chọn hệ tọa độ $Oxyz$ như hình vẽ dưới.

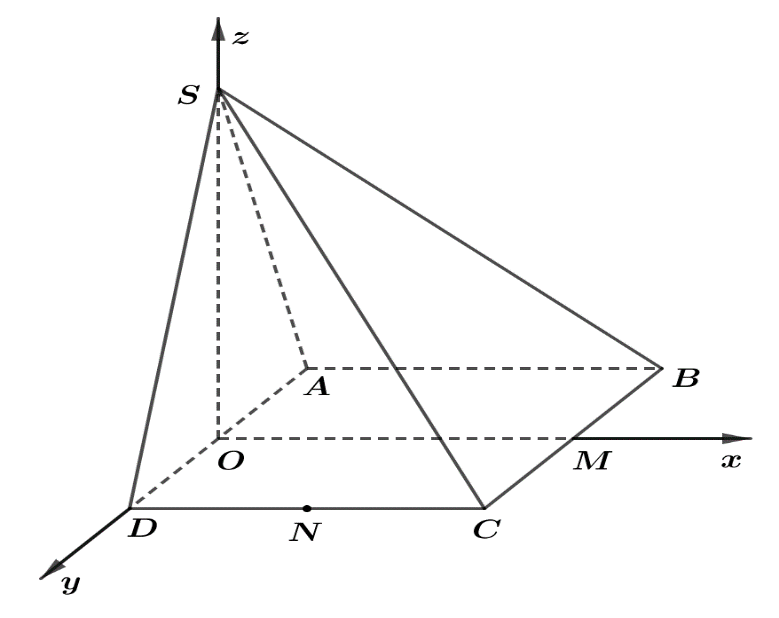
Xác định tọa độ các điểm $S,M,N$ theo $a$.

Lời giải

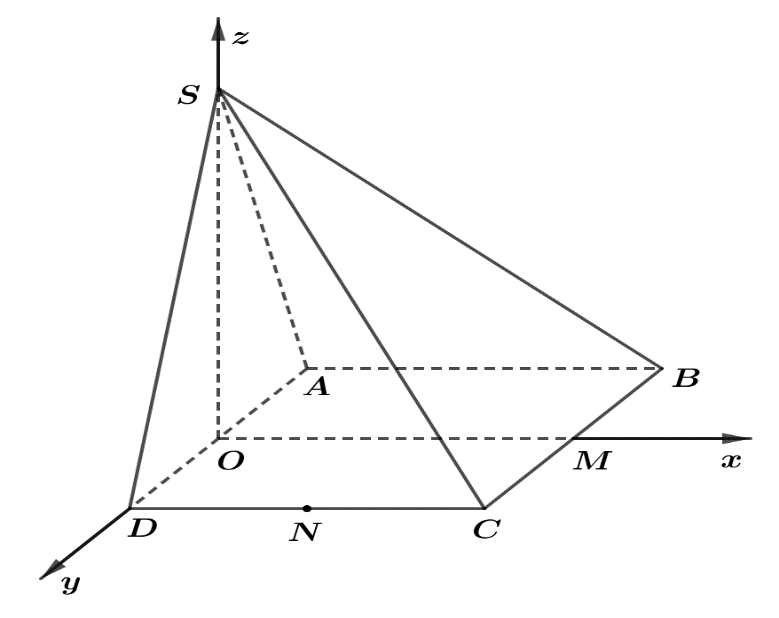
Chọn hệ tọa độ $Oxyz$ như hình vẽ.

$S\left( {0\,;\,0\,;\,\frac{{a\sqrt 3 }}{2}} \right);M\left( {a\,;\,0\,;\,0} \right);\,N\left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right).$.

Ví dụ 4. Cho tứ diện $OABC$, có $OA,OB,OC$đôi một vuông góc và $OA = 5,OB = 2,OC = 4$. Gọi $M,N$ lần lượt là trung điểm của $OB$và $OC$. Gọi $G,K$ lần lượt là trọng tâm của tam giác $ABC$ và $AMN$. Tính khoảng cách từ $G$ đến $K$.

Lời giải

Chọn hệ trục tọa độ $Oxyz$ như hình vẽ.

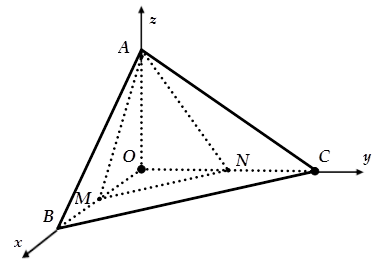
Ta có $O\left( {0;0;0} \right)$, $A \in {\text{Oz}},\;B \in Ox,\;C \in Oy$ sao cho $AO = 5,\;OB = 2,\;OC = 4$

$ \Rightarrow A\left( {0;0;5} \right),\;B\left( {2;0;0} \right),\;C\left( {0;4;0} \right)$.

Khi đó: $G$ là trọng tâm tam giác$ABC$ nên $G\left( {\frac{2}{3};\frac{4}{3};\frac{5}{3}} \right)$

$M$là trung điểm $OB$nên $M\left( {1;0;0} \right)$

$N$là trung điểm $OC$nên $N\left( {0;2;0} \right)$.

$K$ là trọng tâm tam giác$AMN$ nên $K\left( {\frac{1}{3};\frac{2}{3};\frac{5}{3}} \right)$

Khoảng cách từ $G$ đến $K$ là: $GK = \sqrt {{{\left( {\frac{1}{3} – \frac{2}{3}} \right)}^2} + {{\left( {\frac{2}{3} – \frac{4}{3}} \right)}^2} + {{\left( {\frac{5}{3} – \frac{5}{3}} \right)}^2}} = \frac{{\sqrt 5 }}{3}$

Ví dụ 5. Cho hình chóp $S.ABCD$ đáy là hình thang vuông tại $A$ và $D$, $SA \bot \left( {ABCD} \right)$. Góc giữa $SB$ và mặt phẳng đáy bằng ${45^{\text{o}}}$, $E$ là trung điểm của $SD$, $AB = 2a$, $AD = DC = a$. Gọi $G$ là trọng tâm của tam giác $ACE$. Tính độ dài đoạn $BG$.

Lời giải

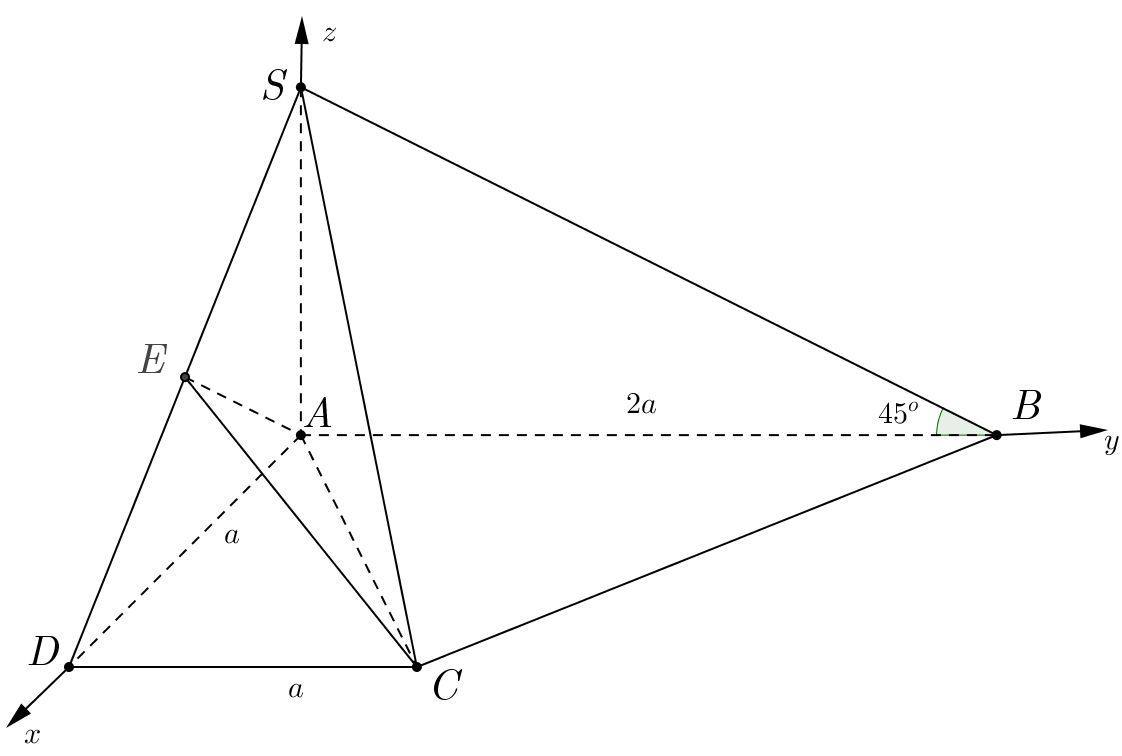
Hình chiếu của $SB$ trên mặt phẳng $\left( {ABCD} \right)$ là $AB$ $ \Rightarrow $ Góc giữa $SB$ và mặt đáy là góc giữa $SB$ và $AB$ và bằng góc $\widehat {SBA} = {45^o}$.

Tam giác $SAB$ vuông cân tại $A$ $ \Rightarrow SA = 2a$.

Chọn hệ trục tọa độ như hình vẽ ta có: $A\left( {0;0;0} \right)$, $B\left( {0;2a;0} \right)$, $C\left( {a;a;0} \right)$, $D\left( {a;0;0} \right)$, $S\left( {0;0;2a} \right)$, $E\left( {\frac{a}{2};0;a} \right)$.

Gọi $G$ là trọng tâm của tam giác $ACE \Rightarrow G\left( {\frac{a}{2};\frac{a}{3};\frac{a}{3}} \right)$

Độ dài $BG$ là: $BG = \sqrt {{{\left( {\frac{a}{2} – 0} \right)}^2} + {{\left( {\frac{a}{3} – 2a} \right)}^2} + {{\left( {\frac{a}{3} – 0} \right)}^2}} = \frac{{a\sqrt {113} }}{6}$

Ví dụ 6. Trong không gian với hệ tọa độ $Oxyz$, cho hình chóp $S.ABCD$, đáy $ABCD$ là hình chữ nhật. Biết $A\left( {0;0;0} \right)$,$D\left( {2;0;0} \right)$,$B\left( {0;4;0} \right)$,$S\left( {0;0;4} \right)$. Gọi $M$ là trung điểm của $SB$ và $G$ là trọng tâm của tam giác $SCD$. Tính độ dài đoạn $MG$.

Lời giải

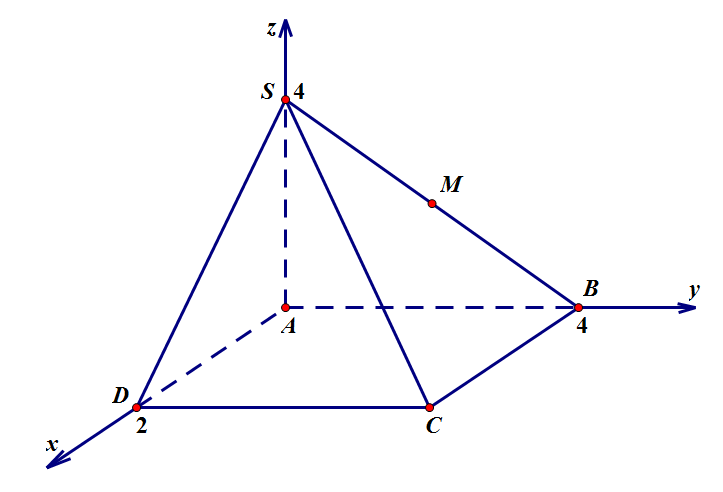
Chọn hệ trục tọa độ như hình vẽ : $A\left( {0;0;0} \right)$,$D\left( {2;0;0} \right)$,$B\left( {0;4;0} \right)$,$S\left( {0;0;4} \right)$.

$M$ là trung điểm của $SB$ $ \Rightarrow M\left( {0;2;2} \right)$.

Tứ giác $ABCD$ là hình chữ nhật nên $\left\{ \begin{gathered}
{x_A} + {x_C} = {x_B} + {x_D} \hfill \\
{y_A} + {y_C} = {y_B} + {y_D} \hfill \\
{z_A} + {z_C} = {z_B} + {z_D} \hfill \\
\end{gathered} \right.$$ \Rightarrow \left\{ \begin{gathered}
{x_C} = 2 \hfill \\
{y_C} = 4 \hfill \\
{z_C} = 0 \hfill \\
\end{gathered} \right.$$ \Rightarrow C\left( {2;4;0} \right)$.

$G$ là trọng tâm của tam giác $SCD$ $ \Rightarrow G\left( {\frac{4}{3};\frac{4}{3};\frac{4}{3}} \right)$

Độ dài $MG$ là: $MG = \sqrt {{{\left( {\frac{4}{3} – 0} \right)}^2} + {{\left( {\frac{4}{3} – 2} \right)}^2} + {{\left( {\frac{4}{3} – 2} \right)}^2}} = \frac{{2\sqrt 6 }}{3}$

Ví dụ 7. Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có các kích thước $AB = 4,\,AD = 3,AA’ = 5$. Gọi $G$ là trọng tâm của tam giác $ACB’$. Tính độ dài đoạn $BG$ là:

Lời giải

Chọn hệ trục tọa độ như hình vẽ.

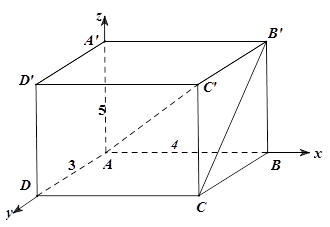
Có $A\left( {0\,0;\,0} \right),C\left( {4;3;0} \right),B’\left( {4;0;5} \right),B\left( {4;0;0} \right)$,

$G$ là trọng tâm của tam giác $ACB’$$ \Rightarrow G\left( {\frac{8}{3};1;\frac{5}{3}} \right)$

Độ dài $BG$ là: $BG = \sqrt {{{\left( {\frac{8}{3} – 4} \right)}^2} + {{\left( {1 – 0} \right)}^2} + {{\left( {\frac{5}{3} – 0} \right)}^2}} = \frac{{5\sqrt 2 }}{3}$

Ví dụ 8. Cho tứ diện $ABCD$ có $AB\,,AC\,,AD$ đôi một vuông góc với nhau và $AD = 2\,,AB = AC = 1$. Gọi $I$ là trung điểm của đoạn thẳng $BC$ và $G$ là trọng tâm của tam giác $ABD$. Tính độ dài $BI$.

Lời giải

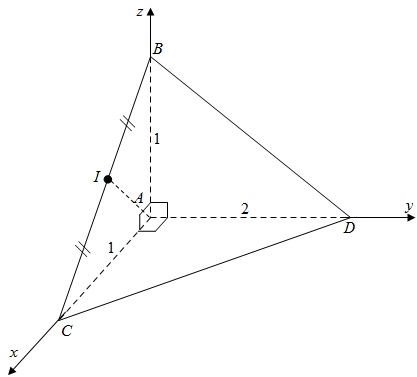
Vì tứ diện $ABCD$ có $AB\,,AC\,,AD$ đôi một vuông góc với nhau, nên ta chọn hệ trục tọa độ $Axyz$ như hình vẽ (với $A$ là gốc tọa độ, đường thằng $AC$ nằm trên trục $Ax$, $AD$ nằm trên trục $Ay$ và $AB$ nằm trên trục $Az$).

Từ đó suy ra: $A\left( {0\,;0\,;0} \right)$, $B\left( {0\,;0\,;1} \right)$ vì $B \in Az$, $C\left( {1\,;0\,;0} \right)$ vì $C \in Ax$, $D\left( {0\,;\,2\,;0} \right)$ vì $D \in Ay$.

Vì $I$ là trung điểm của $BC$ nên $I\left( {\frac{1}{2}\,;0\,;\frac{1}{2}} \right)$.

$G$ là trọng tâm của tam giác $ABD \Rightarrow G\left( {\frac{1}{6}\,;0\,;\frac{1}{2}} \right)$

Độ dài $BI$ là: $BI = \sqrt {{{\left( {\frac{1}{2} – \frac{1}{6}} \right)}^2} + {{\left( {0 – 0} \right)}^2} + {{\left( {\frac{1}{2} – \frac{1}{2}} \right)}^2}} = \frac{1}{3}$

Ví dụ 9. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA = a$ và vuông góc với mặt phẳng đáy. Gọi $M,N$ lần lượt là trung điểm của $SB$ và $SD$ và $G$ là trọng tâm của tam giác $AMN$ . Tính tọa độ điểm $G$.

Lời giải

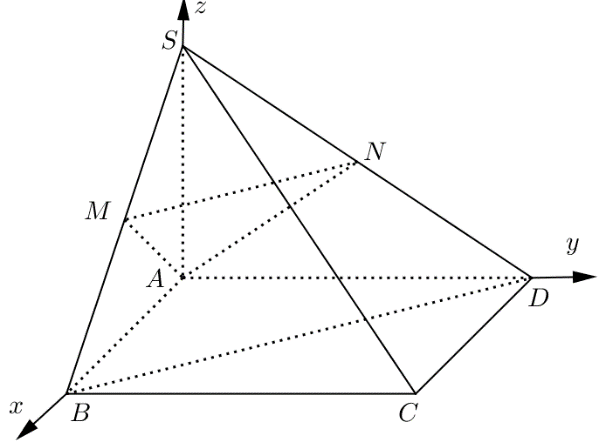
Chọn hệ trục tọa độ $Oxyz$ thỏa mãn: $A \equiv O,\,B\left( {a;0;0} \right),D\left( {0;a;0} \right),S\left( {0;0;a} \right)$(như minh họa hình vẽ),

suy ra $M\left( {\frac{a}{2};0;\frac{a}{2}} \right)$ và$N\left( {0;\frac{a}{2};\frac{a}{2}} \right)$.

$G$ là trọng tâm của tam giác $AMN$$ \Rightarrow G\left( {\frac{a}{6};\frac{a}{6};\frac{a}{3}} \right)$

Ví dụ 10. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Gọi $G$ là trọng tâm của tam giác $A’BD$. Tính độ dài $C’G$.

Lời giải

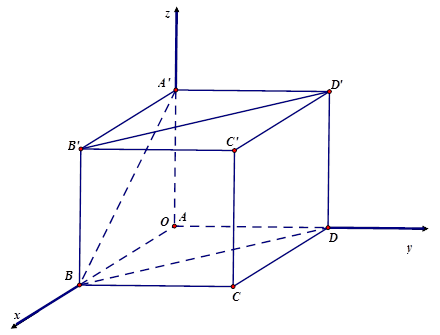
Chọn hệ trục tọa độ $Oxyz$ với $A \equiv O\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)\,$, $C\left( {a;a;0} \right)\,$, $D\left( {0;a;0} \right)$, $A’\left( {0;0;a} \right)\,,\,$

$B’\left( {a;0;a} \right)\,,\,$$C’\left( {a;a;a} \right)$, $D’\left( {0;a;a} \right)$

$G$ là trọng tâm của tam giác $A’BD$$ \Rightarrow G\left( {\frac{a}{3};\frac{a}{3};\frac{a}{3}} \right)$

Độ dài $C’G$ là: $C’G = \sqrt {{{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{a}{3} – a} \right)}^2}} = \frac{{2a\sqrt 3 }}{3}$

Ví dụ 11. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a$, $BC = a\sqrt 3 $, $SA = a$ và $SA$ vuông góc với đáy $ABCD$. Gọi $G$ là trọng tâm của tam giác $SBD$. Tính độ dài $CG$.

Lời giải

Đặt hệ trục tọa độ $Oxyz$ như hình vẽ.

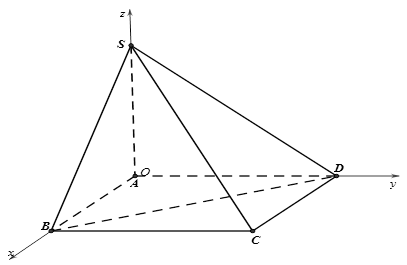
Khi đó, ta có:

$A\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)$, $C\left( {a;a\sqrt 3 ;0} \right)$, $D\left( {0;a\sqrt 3 ;0} \right)$, $S\left( {0;0;a} \right)$.

$G$ là trọng tâm của tam giác $SBD$$ \Rightarrow G\left( {\frac{a}{3};\frac{{a\sqrt 3 }}{3};\frac{a}{3}} \right)$

Độ dài $CG$ là: $CG = \sqrt {{{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3} – a\sqrt 3 } \right)}^2} + {{\left( {\frac{a}{3} – 0} \right)}^2}} = \frac{{a\sqrt {17} }}{3}$

Ví dụ 12. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông có độ dài đường chéo bằng $a\sqrt 2 $ và $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $\alpha $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$. Nếu $\tan \alpha = \sqrt 2 $ thì tọa độ điểm $I$ là bao nhiêu? Biết $I = AC \cap BD$ và chọn hệ trục tọa độ $Oxyz$ như hình vẽ dưới.

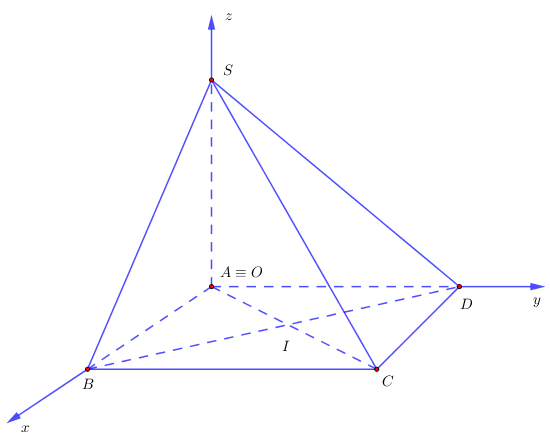
Lời giải

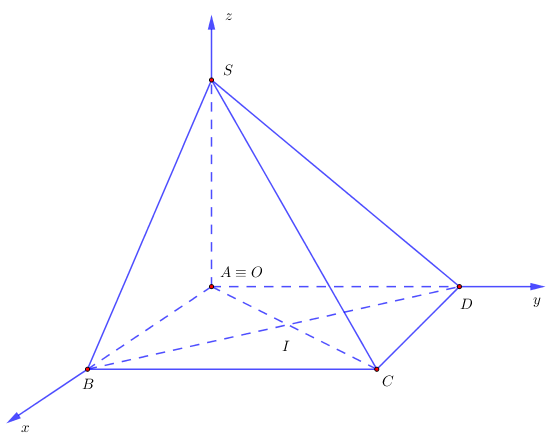
Gọi $I = AC \cap BD$.

Hình vuông $ABCD$ có độ dài đường chéo bằng $a\sqrt 2 $ suy ra hình vuông đó có cạnh bằng $a$.

Ta có $\left\{ \begin{gathered}
\left( {SBD} \right) \cap \left( {ABCD} \right) = BD \hfill \\
SI \bot BD \hfill \\
AI \bot BD \hfill \\
\end{gathered} \right.$$ \Rightarrow \widehat {\left( {\left( {SBD} \right);\,\left( {ABCD} \right)} \right)} = \widehat {\left( {SI;\,AI} \right)} = \widehat {SIA}$.

Ta có $\tan \alpha = \tan \widehat {SIA} = \frac{{SA}}{{AI}} \Leftrightarrow SA = a$.

Chọn hệ trục tọa độ $Oxyz$ như hình vẽ. Ta có $A\left( {0;\,0;\,0} \right)$, $B\left( {a;\,0;\,0} \right)$, $C\left( {a;\,a;\,0} \right)$, $S\left( {0;\,0;\,a} \right)$.

$ \Rightarrow I\left( {\frac{a}{2};0;\frac{a}{2}} \right)$

Ví dụ 13. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $G$ là trọng tâm của tam giác $SAB$ và $M,\,N$ lần lượt là trung điểm của $SC,\,SD$. Chọn hệ trục tọa độ $Oxyz$ như hình vẽ dưới, Tính tọa độ các điểm $G,M,\,N$theo $a$.

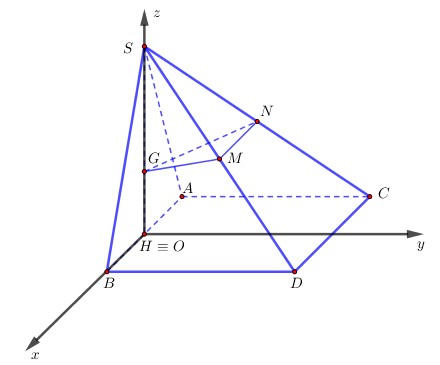
Lời giải

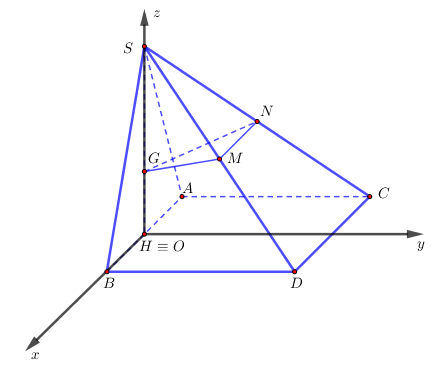
Chọn hệ trục tọa độ $Oxyz$ như hình vẽ. Khi đó

$S\left( {0;\,0;\,\frac{{\sqrt 3 }}{2}} \right)$; $A\left( {\frac{{ – a}}{2};0;\,0} \right)$; $B\left( {\frac{a}{2};0;\,0} \right)$;$C\left( {\frac{a}{2};a;\,0} \right)$; $D\left( {\frac{{ – a}}{2};a;\,0} \right)$

suy ra $G\left( {0;\,0;\,\frac{{a\sqrt 3 }}{6}} \right)$; $M\left( {\frac{a}{4};\frac{a}{2};\,\frac{{a\sqrt 3 }}{4}} \right)$; $N\left( { – \frac{a}{4};\frac{a}{2};\,\frac{{a\sqrt 3 }}{4}} \right)$

Ví dụ 14. Cho hình chóp $O.ABC$ có ba cạnh $OA$, $OB$, $OC$ đôi một vuông góc và $OA = OB = OC = a$. Gọi $M$ là trung điểm cạnh $AB$. Tính góc tạo bởi hai vectơ $\overrightarrow {BC} $ và $\overrightarrow {OM} $.

Lời giải

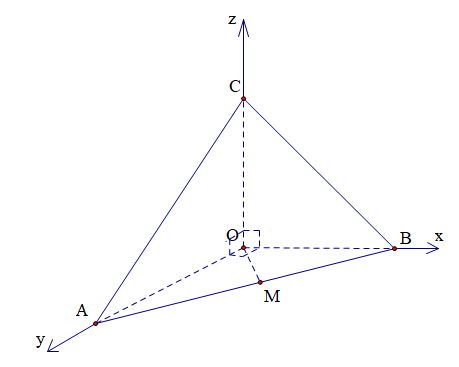
Chọn hệ trục tọa độ $Oxyz$ như hình vẽ.

Ta có: $O\left( {0\,;\,0\,;\,0} \right)$, $A\left( {0\,;\,a\,;\,0} \right)$, $B\left( {a\,;\,0\,;\,0} \right)$, $C\left( {0\,;\,0\,;\,a} \right)$, $M\left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right)$.

Khi đó ta có: $\overrightarrow {BC} = \left( { – a\,;\,0\,;\,a} \right)$,$\overrightarrow {OM} = \left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right)$

$ \Rightarrow $ $\cos \left( {\overrightarrow {BC} \,;\,\overrightarrow {OM} } \right)$ $ = \frac{{\overrightarrow {BC} .\overrightarrow {OM} }}{{BC.OM}}$$ = \frac{{ – \frac{{{a^2}}}{2}}}{{a.\sqrt 2 .\frac{{a\sqrt 2 }}{2}}}$$ = – \frac{1}{2}$$ \Rightarrow $$\left( {\overrightarrow {BC} \,;\,\overrightarrow {OM} } \right) = 120^\circ $.

Ví dụ 15. Cho hình chóp tứ giác đều $S.ABCD$ có $AB = a$, $SA = a\sqrt 2 $. Gọi $G$ là trọng tâm tam giác $SCD$. Tính $cosin$ góc giữa đường thẳng $BG$ với đường thẳng $SA$.

Lời giải

Gọi $O = AC \cap BD$.

Tam giác $SAO$ vuông : $SO = \sqrt {S{A^2} – A{O^2}} = \frac{{a\sqrt 6 }}{2}$

Gắn tọa độ như hình vẽ

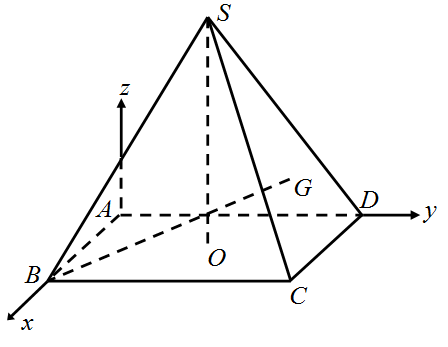
$A\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)$, $C\left( {a;a;0} \right)$, $D\left( {0;a;0} \right)$, $O\left( {\frac{a}{2};\frac{a}{2};0} \right)$, $S\left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)$.

Vì $G$ là trọng tâm tam giác $SCD$ nên $G\left( {\frac{a}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right)$.

Ta có : $\overrightarrow {AS} = \left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)$ $ = \frac{a}{2}\left( {1;1;\sqrt 6 } \right)$, $\overrightarrow {BG} = \left( {\frac{{ – a}}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right) = \frac{a}{6}\left( { – 3;5;\sqrt 6 } \right)$.

Góc giữa đường thẳng $BG$ với đường thẳng $SA$ bằng:

$\cos \left( {BG;SA} \right) = \frac{{\left| {\overrightarrow {BG} .\overrightarrow {AS} } \right|}}{{BG.AS}} = \frac{{\left| { – 3 + 5 + 6} \right|}}{{\sqrt {40} .\sqrt 8 }} = \frac{{\sqrt 5 }}{5}$.

Ví dụ 16. Cho hình chóp $S.ABCD$ có đáy hình vuông. Cho tam giác $SAB$ vuông tại $S$ và góc $SBA$ bằng ${30^0}$. Mặt phẳng $\left( {SAB} \right)$ vuông góc mặt phẳng đáy. Gọi $M,N$ là trung điểm $AB,BC$. Tìm cosin góc tạo bởi hai đường thẳng $\left( {SM,DN} \right)$.

Lời giải

Trong $\left( {SAB} \right)$, kẻ $SH \bot AB$ tại $H$.

Ta có: $\left\{ \begin{gathered}
\left( {SAB} \right) \bot \left( {ABCD} \right) \hfill \\
\left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \\
SH \subset \left( {SAB} \right),SH \bot AB \hfill \\
\end{gathered} \right. \Rightarrow SH \bot \left( {ABCD} \right)$.

Kẻ tia $Az$//$SH$ và chọn hệ trục tọa độ $Axyz$ như hình vẽ sau đây.

Trong tam giác $SAB$ vuông tại $S$, $SB = AB.\cos \widehat {SBA} = a.\cos {30^0} = \frac{{a\sqrt 3 }}{2}$.

Trong tam giác $SBH$ vuông tại $H$, $BH = SB.\cos \widehat {SBH} = \frac{{3a}}{4}$ và $SH = BH.\sin \widehat {SBA} = \frac{{a\sqrt 3 }}{4}$.

$AH = AB – BH = a – \frac{{3a}}{4} = \frac{a}{4}$ $ \Rightarrow H\left( {0;\frac{a}{4};0} \right) \Rightarrow S\left( {0;\frac{a}{4};\frac{{a\sqrt 3 }}{4}} \right)$.

$M\left( {0;\frac{a}{2};0} \right)$, $D\left( {a;0;0} \right)$, $N\left( {\frac{a}{2};a;0} \right)$.

Ta có: $\overrightarrow {SM} = \left( {0;\frac{a}{4}; – \frac{{a\sqrt 3 }}{4}} \right)$, $\overrightarrow {DN} = \left( { – \frac{a}{2};a;0} \right)$

$ \Rightarrow $$\cos \left( {SM,DN} \right) = \frac{{\left| {\overrightarrow {SM} .\overrightarrow {DN} } \right|}}{{SN.DN}} = \frac{{\frac{{{a^2}}}{4}}}{{\frac{a}{2}.\frac{{a\sqrt 5 }}{2}}} = \frac{1}{{\sqrt 5 }}$.

———-